GXBeam
Pure Julia Implementation of Geometrically Exact Beam Theory
Author: Taylor McDonnell
GXBeam is a pure Julia implementation of Geometrically Exact Beam Theory, originally based on the open source code GEBT and its associated papers[1][2], though it has since been augmented with a number of additional features.
As a sample of one of the many things this package can do, here's a time domain simulation of the dynamic response of a joined wing subjected to a simulated gust, scaled up in order to visualize the deflections: 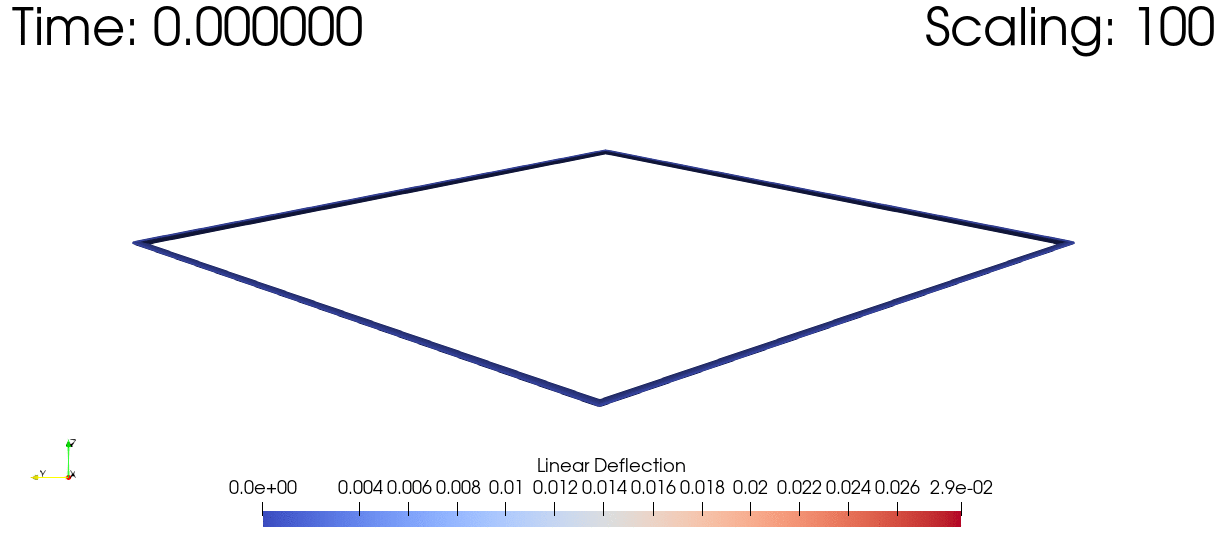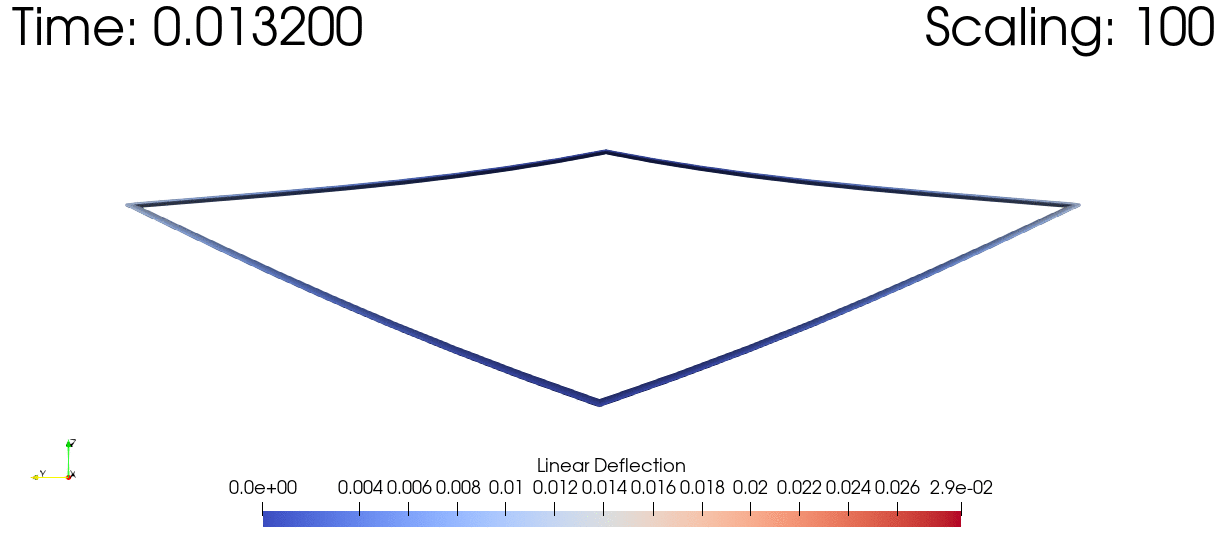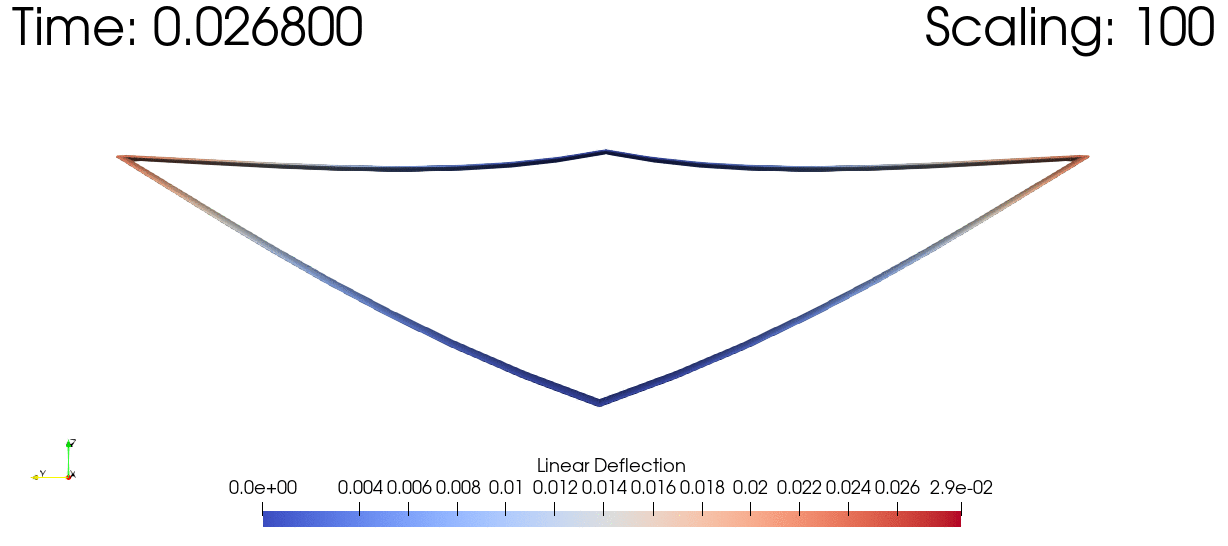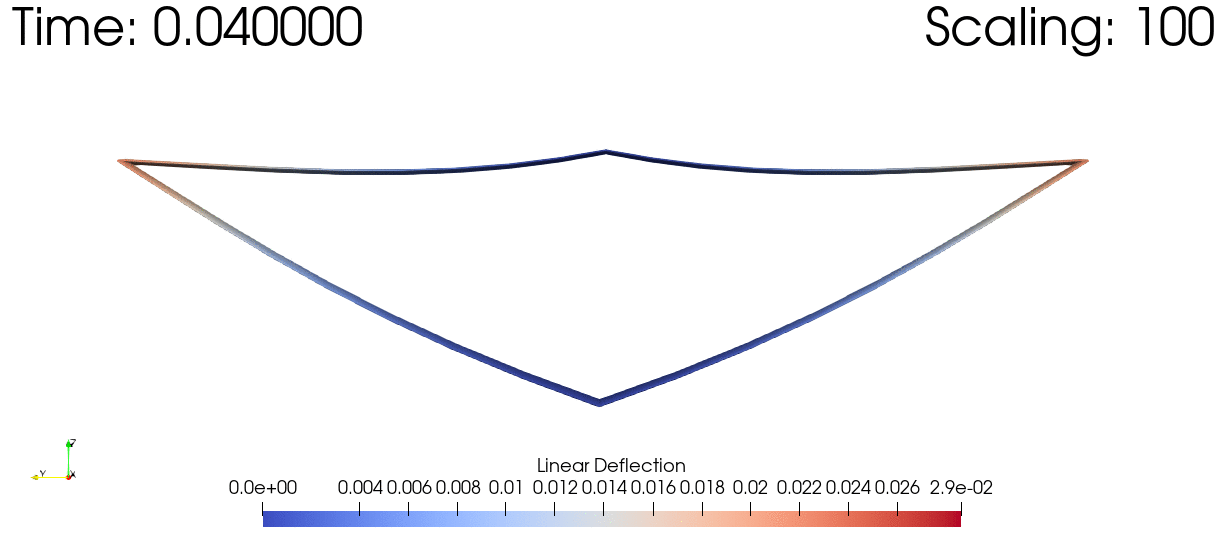
And here's a dynamic simulation of a wind turbine subjected to a sinusoidal tip load. 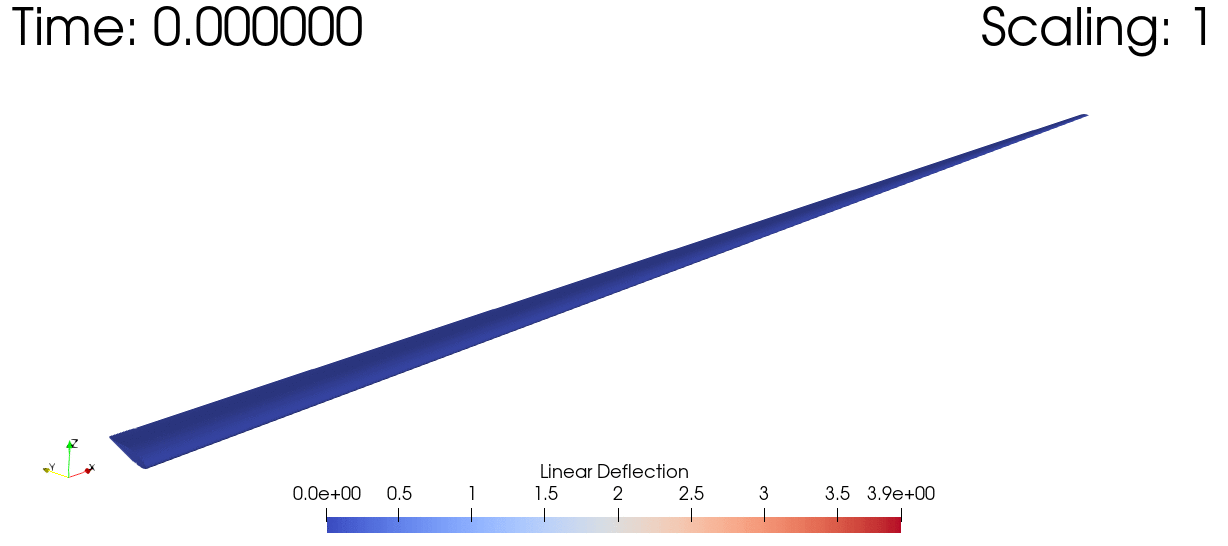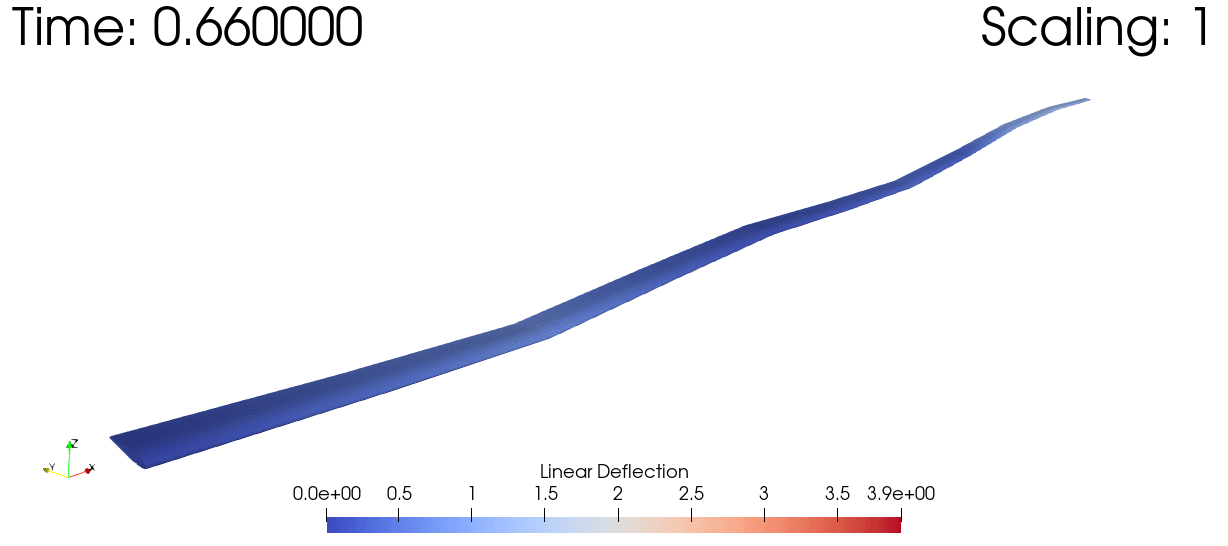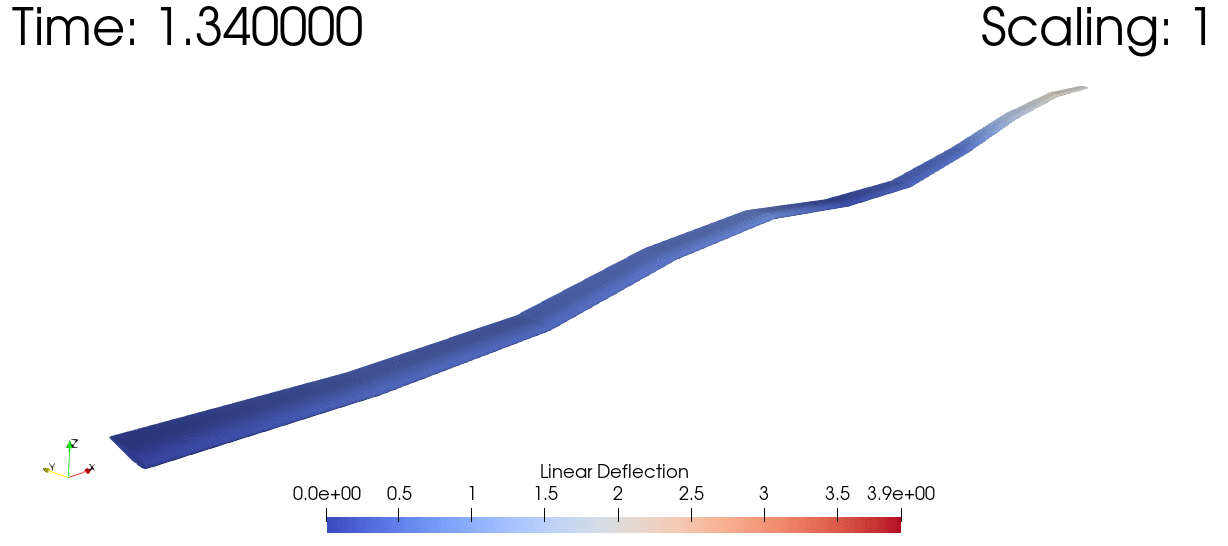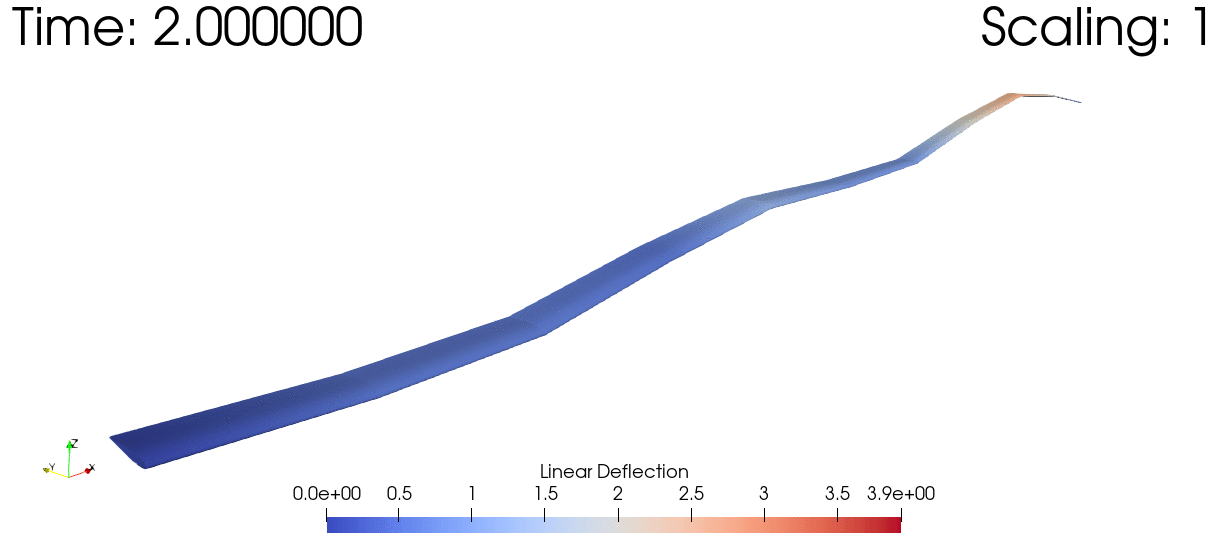
Package Features
- Performs multiple types of analyses including:
- Linear/Nonlinear static analyses
- Linear/Nonlinear steady-state analyses
- Linear/Nonlinear eigenvalue analyses (by linearizing about a steady state condition)
- Linear/Nonlinear time-marching dynamic analyses
- Accurately models arbitrary systems of interconnected highly flexible composite beams.
- Captures all geometric nonlinearities due to large deflections and rotations (subject to a small strain assumption)
- Models angular displacements of any magnitude using only three parameters
- Uses the full 6x6 Timoshenko beam stiffness matrix
- Calculate section compliance and inertia matrices and compute strain recovery
- Uses quadrilateral finite elements rather than classical lamiante theory for much better accuracy and cross coupling
- Allows for general geometry with inhomogenous properties and anisotropic behavior (computes full 6x6 matrix)
- Ply materials are general orthotropic
- Provides convenience method for paramterizing airfoil layups
- Strain recovery functionality to compute stresses and strains on the mesh using the results of the beam solution
- Tsai-wu failure criteria
- Models time-varying distributed forces/moments including
- Point and distributed loads which remain fixed in the body-frame
- Point and distributed loads which rotate with the structure
- Loads due to known body frame velocities and accelerations
- Gravitational loads acting on beam elements and point masses
- Loads resulting from stiffness-proportional structural damping
- Optional DifferentialEquations interface.
- Constant mass matrix differential algebraic equation formulation
- Fully implicit differential algebraic equation formulation
- Provides derivatives with ForwardDiff (including overloading internal solvers with implicit analytic methods)
- Result visualization using WriteVTK
- Verified and validated against published analytical and computational results. See the examples in the documentation.
Installation
Enter the package manager by typing ] and then run the following:
pkg> add GXBeamPerformance
This code has been optimized to be highly performant. In our tests we found that GXBeam outperforms GEBT by a significant margin across all analysis types, as seen in the following table. More details about the specific cases which we test may be found by inspecting the scripts and input files and scripts for these tests in the benchmark folder.
| Package | Steady Analysis | Eigenvalue Analysis | Time Marching Analysis |
|---|---|---|---|
| GEBT | 13.722 ms | 33.712 ms | 26.870 s |
| GXBeam | 4.716 ms | 18.478 ms | 9.019 s |
Usage
See the guide.
Limitations
By using the simplest possible shape functions (constant or linear shape functions), this package avoids using numerical quadrature except when integrating applied distributed loads (which can be pre-integrated). As a result, element properties are approximated as constant throughout each beam element and a relatively large number of beam elements may be necessary to achieve grid-independent results. More details about the convergence of this package may be found in the examples.
This package does not currently model cross section warping, and therefore should not be used to model open cross sections (such as I, C, or L-beams). The one exception to this rule is if the beam's width is much greater than its height, in which case the beam may be considered to be strip-like (like a helicopter blade).
This package relies on the results of linear cross-sectional analyses. Most notably, it does not model the nonlinear component of the Trapeze effect, which is the tendency of a beam to untwist when subjected to axial tension. This nonlinear effect is typically most important when modeling rotating structures such as helicopter blades due to the presence of large centrifugal forces. It is also more important when modeling strip-like beams than for modeling closed cross-section beams due to their low torsional rigidity.
Related Codes
GEBT: Open source geometrically exact beam theory code developed in Fortran as a companion to the proprietary cross sectional analysis tool VABS. The theory for this code is provided in references 1 and 2. GXBeam was originally developed based on this package and its associated papers, but has since been augmented with additional features.
BeamDyn: Open source geometrically exact beam theory code developed in Fortran by NREL as part of the OpenFAST project. This code was also developed based on GEBT, but uses Legendre spectral finite elements. This allows for exponential rather than algebraic convergence when the solution is smooth. This makes this code a good candidate for use when analyzing beams with smoothly varying properties. Unfortunately, the code is limited to analyzing a single beam, rather than an assembly of beams.
The cross sectional analysis uses the same underlying theory as in BECAS, but was written to be fast and optimization-friendly. VABS and PreComp are other popular tools for composite cross sectional analysis. The former is not freely available, whereas the latter is lower fidelity as it is based on classical laminate theory.
Contributing
Contributions are welcome and encouraged. If at any point you experience issues or have suggestions related to this package, create a new Github issue so we can discuss it. If you're willing to help solve an issue yourself, we encourage you to create a fork of this repository and submit a pull request with the requested change. Pull requests should generally also add a unit test in test/runtests.jl to ensure that issues do not reoccur along with future changes.
References
[1] Yu, W., & Blair, M. (2012). GEBT: A general-purpose nonlinear analysis tool for composite beams. Composite Structures, 94(9), 2677-2689.
[2] Wang, Q., & Yu, W. (2017). Geometrically nonlinear analysis of composite beams using Wiener-Milenković parameters. Journal of Renewable and Sustainable Energy, 9(3), 033306.
[3] Hodges, D. (2006). Nonlinear Composite Beam Theory. American Institute of Aeronautics and Astronautics.

