Convergence
The following is a compilation of convergence studies found in the literature using FLOWUnsteady.
Wing Performance
Source: E. J. Alvarez, 2022[1]

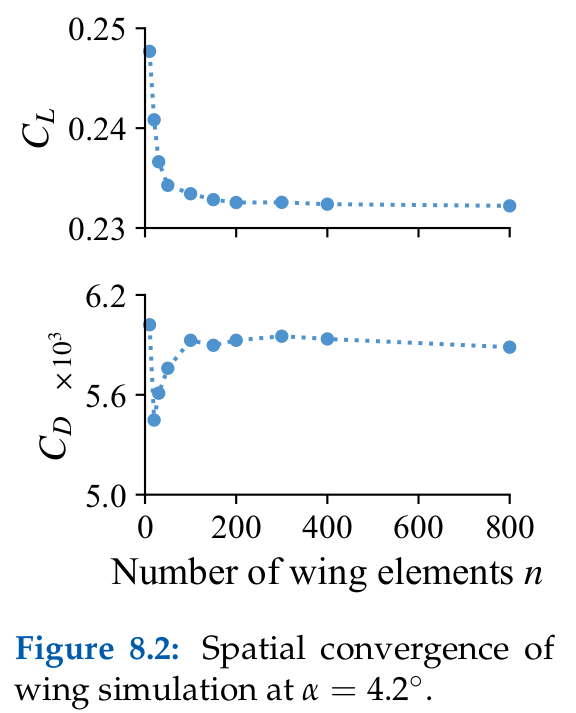
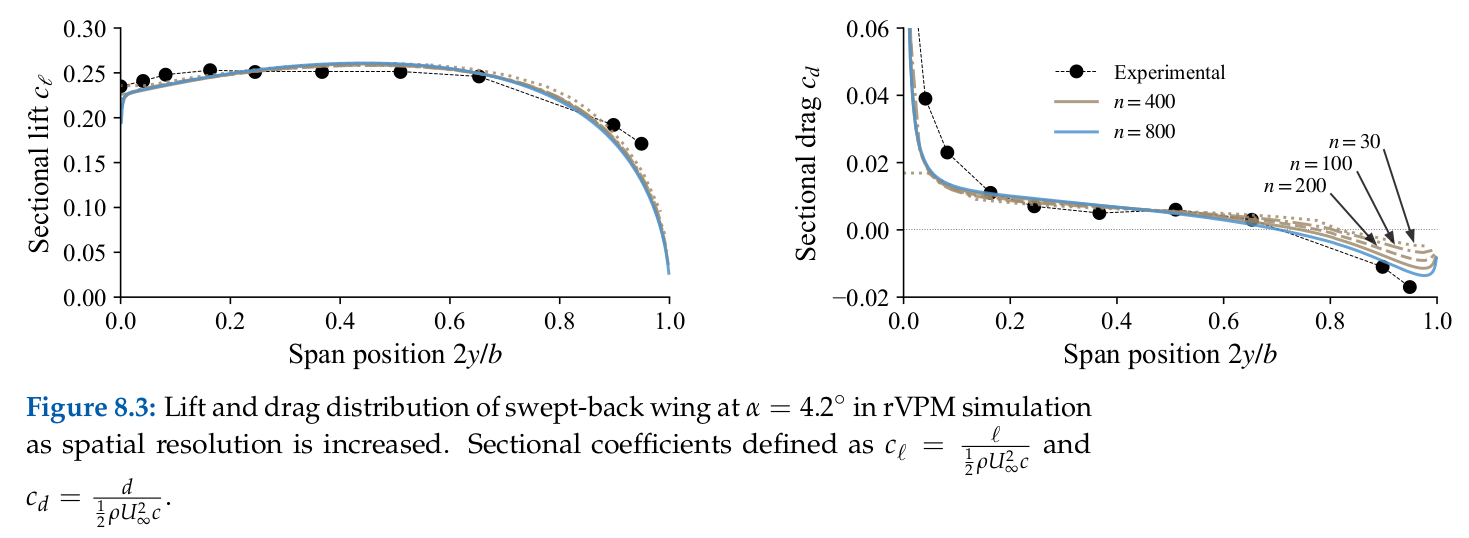
Case: $45^\circ$ swept-back wing at an angle of attack of $4.2^\circ$. Aspect ratio of 5.0, RAE 101 airfoil section with 12% thickness, no dihedral, twist, nor taper. Freestream velocity of $49.7,\mathrm{m/s}$, corresponding to a chord-based Reynolds number of $1.7 \times 10^6$. Convergence of loading distribution and integrated lift and drag as the number of wing elements is increased.
Takeaways:
- Resolving the wake for about 1.5 span-distances is sufficient to converge wing loading
- Using between 100 and 200 elements fully resolves the wing loading ($C_D$ changes by less than 1% with $n_\mathrm{wing} > 100$)

|
|
Rotor Performance
APC 10x7 Propeller Case
Source: E. J. Alvarez and A. Ning, 2020[2]
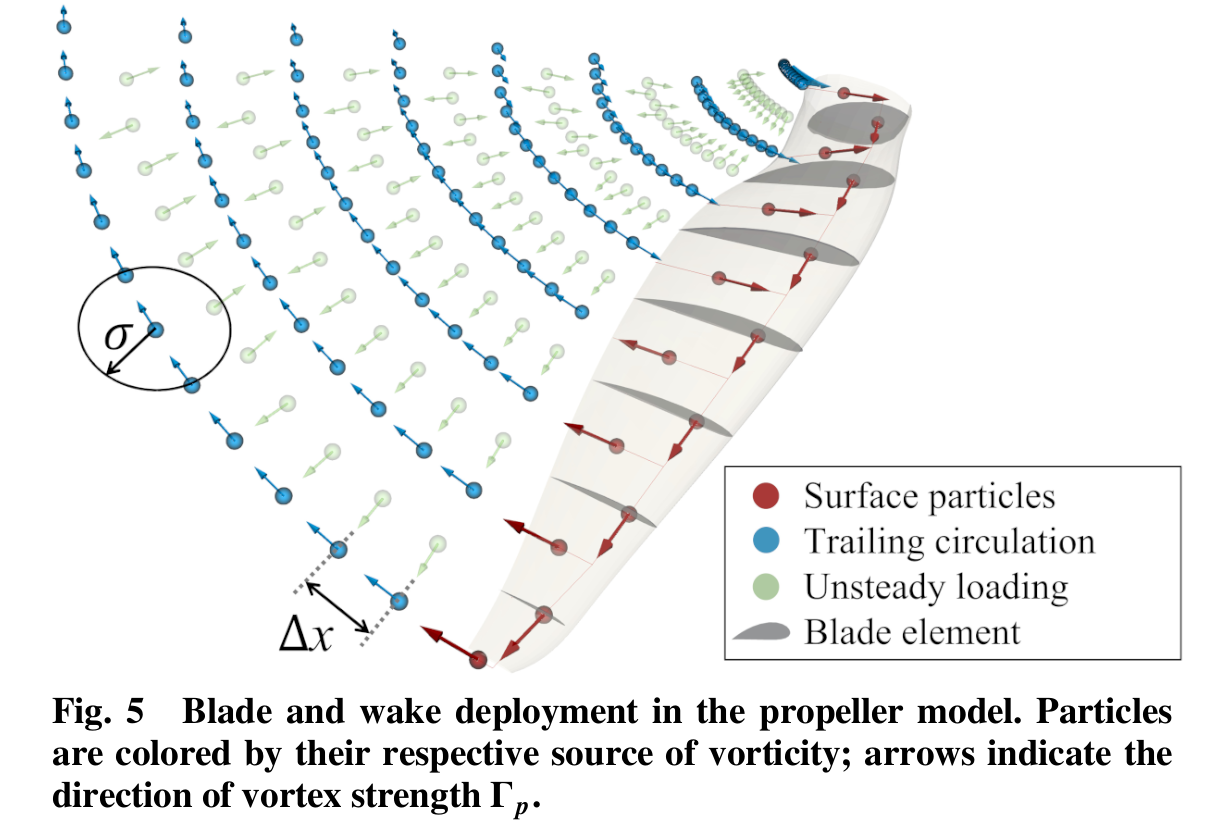
Case: APC 10x7E propeller at an advance ratio of 0.6, tip Mach number of 0.36, and $\mathrm{Re}_c = 6.2 \times 10^4$ and $\mathrm{Re}_D = 6.5 \times 10^5$. Convergence of thrust w.r.t. the following parameters:
- $N_\mathrm{steps}$, number of time steps per revolution.
- $N_\mathrm{sheds}$, number of particle sheds per revolution.
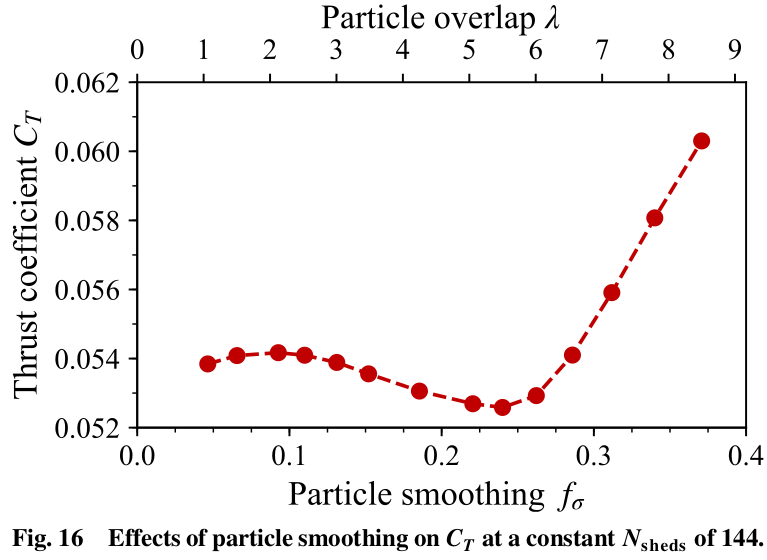
- $\lambda$, core overlap between tip particles defined as $\lambda=\frac{\sigma}{\Delta x}$. Also controlled with the particle smoothing factor $f_\sigma = \sigma/R$, .
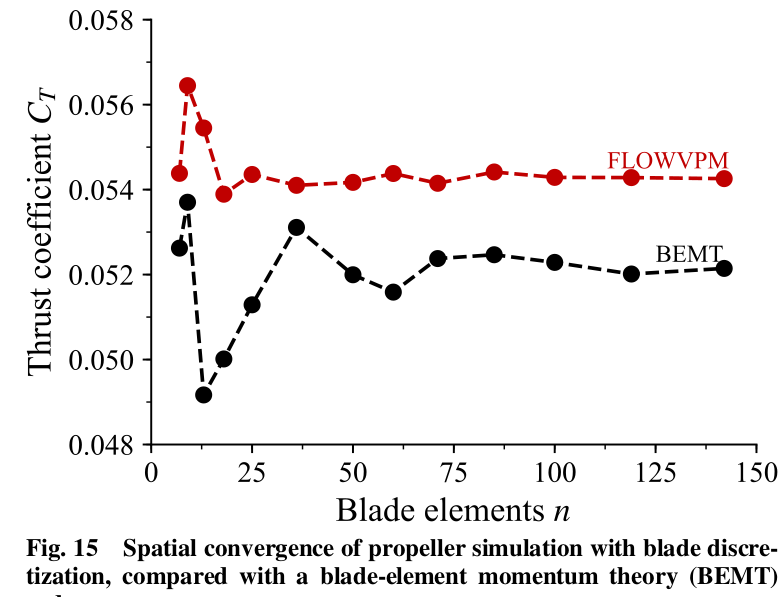
- $n$, number of blade elements per blade.
Default values: $N_\mathrm{steps}=72$, $N_\mathrm{sheds}=144$, $\lambda=2.125$ (or $f_\sigma=0.093$), and $n=50$ as each parameter is independently varied.
Takeaways:
- Temporal discretization error less than 1% with $N_\mathrm{steps} \geq 72$ (or time step smaller than $5^\circ$)
- Spatial discretization error less than 1% with $N_\mathrm{sheds} \geq 144$ and $n = 50$.
- $C_T$ starts to diverge as the stability threshold ($\lambda=1$) is approached, while also diverging as $f_\sigma>0.25$ (equivalent to $\sigma$ larger than $0.25R$) leads to unphysical wake dynamics caused by excessive smoothing. Since the instability associated with $\lambda\rightarrow1$ plateaus at $\lambda\approx2$, we recommend using $\lambda \approx 2.125$ whenever possible.

|
|
Wind Turbine Case
Source: J. Mehr, E. J. Alvarez, and A. Ning, 2022[4]

Case: Test series "H" from UAE study at US Department of Energy.
Takeaways:
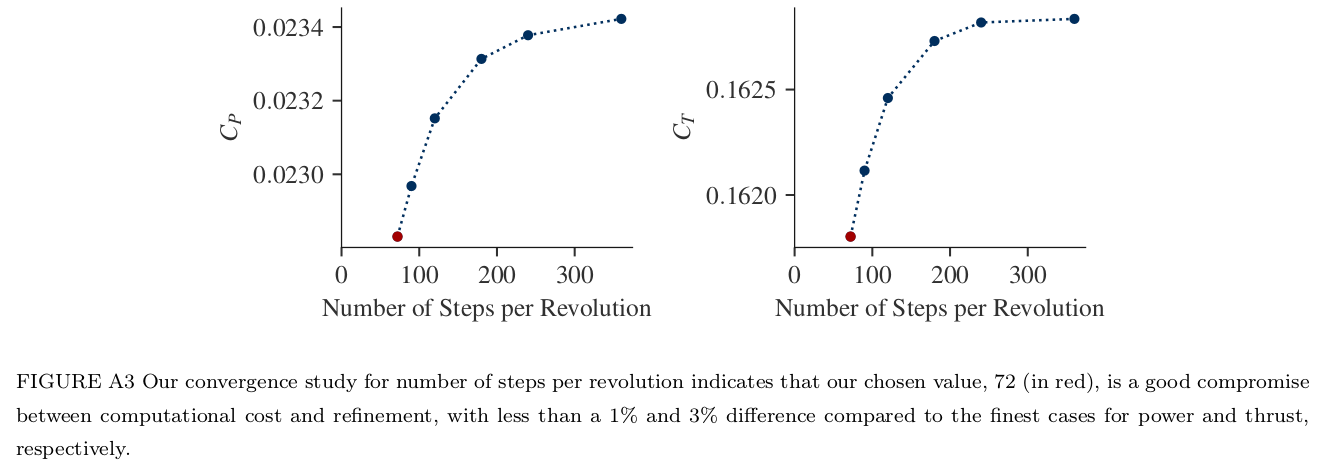
- Spatio-temporal discretization error on thrust $C_T$ is less than 1% with 72 steps per revolution (or $5^\circ$ per step), while error on power $C_P$ is less than 3%.
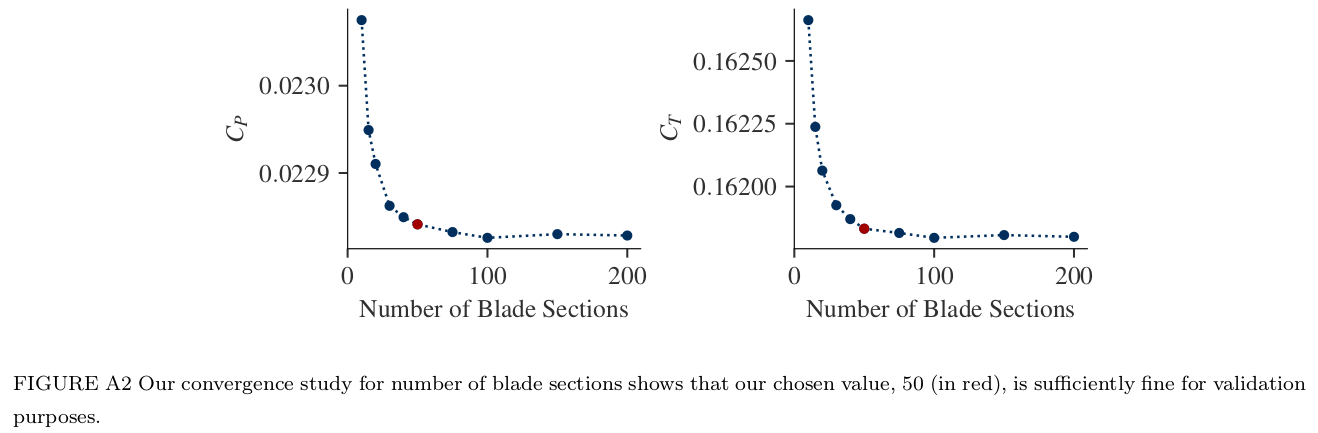
- Blade discretization error less than 0.1% with 50 blade elements per blade.
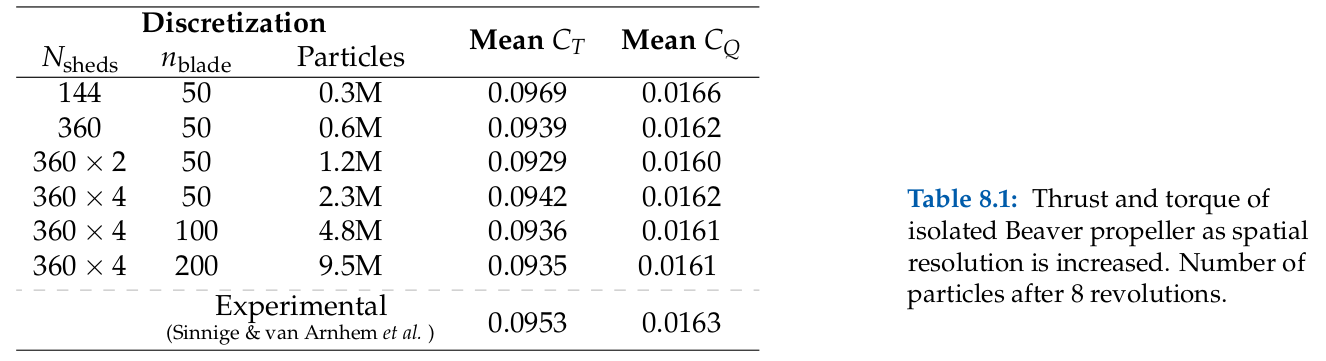
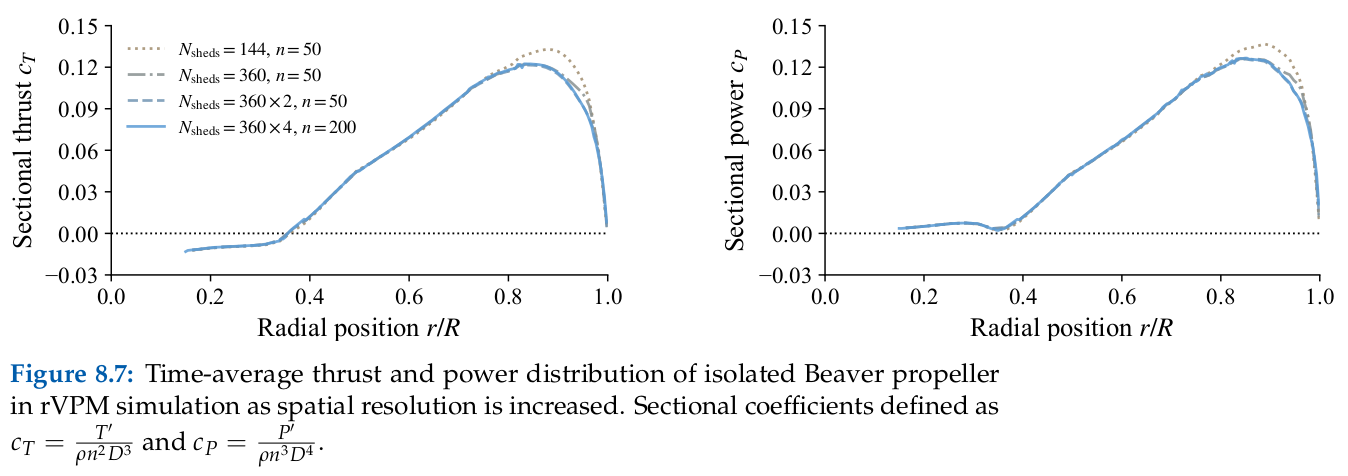
Beaver Propeller Case
Source: E. J. Alvarez, 2022[1], and E. J. Alvarez and A. Ning, 2023[3]

Case: Beaver propeller at an advance ratio of 0.8, tip Mach number of 0.46, and $\mathrm{Re}_{0.7D} = 1.8 \times 10^6$. Convergence of thrust, torque, and blade loading w.r.t. the following parameters:
- $N_\mathrm{sheds}$, number of particle sheds per revolution.
- $n$, number of blade elements per blade.
Constant parameters: $N_\mathrm{steps}=72$ and $\lambda=\frac{\sigma}{\Delta x} = \frac{\sigma N_\mathrm{sheds}}{2\pi R} = 2.125$, which leads to a decreasing $\sigma$ as $N_\mathrm{sheds}$increases.

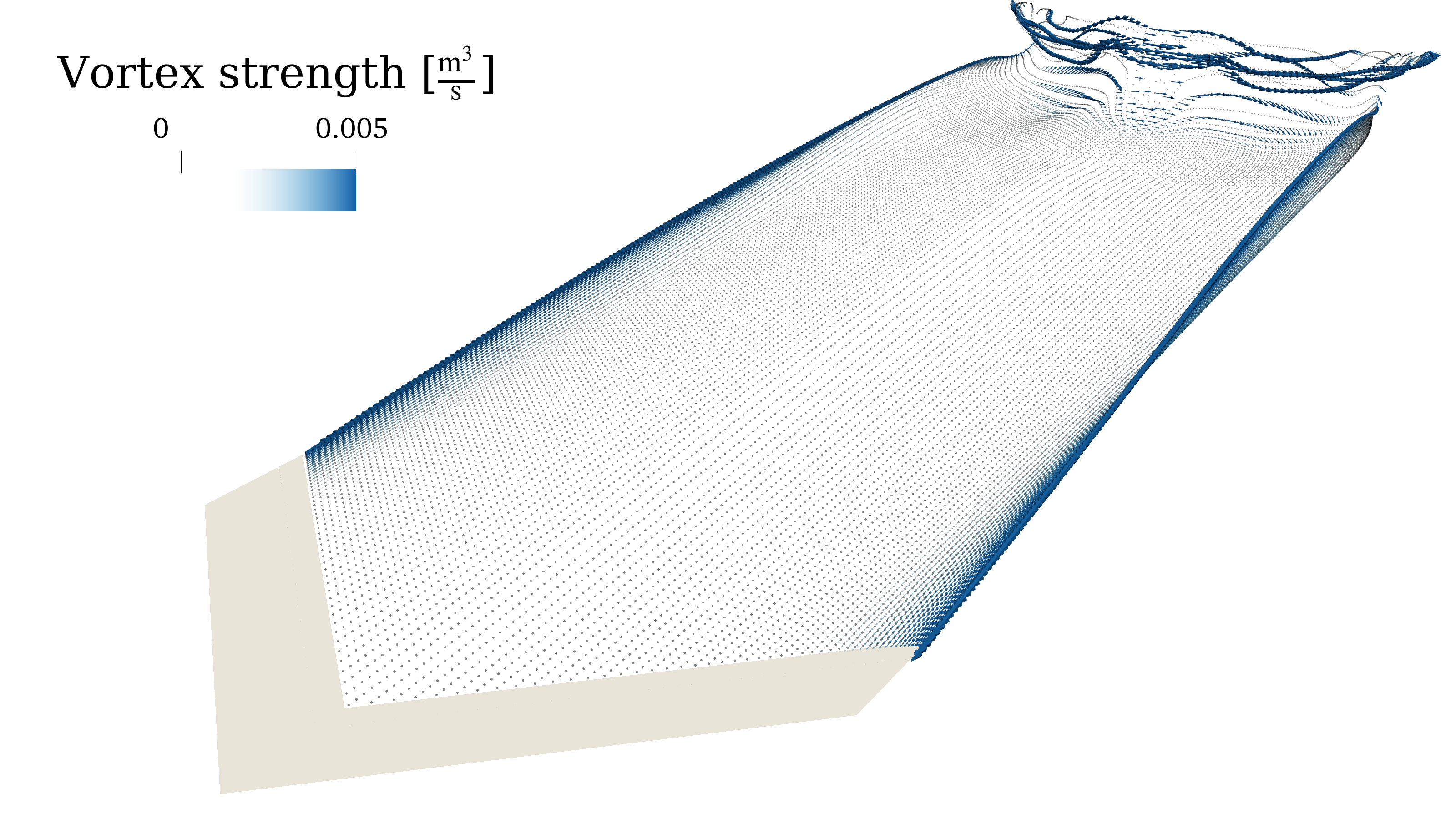
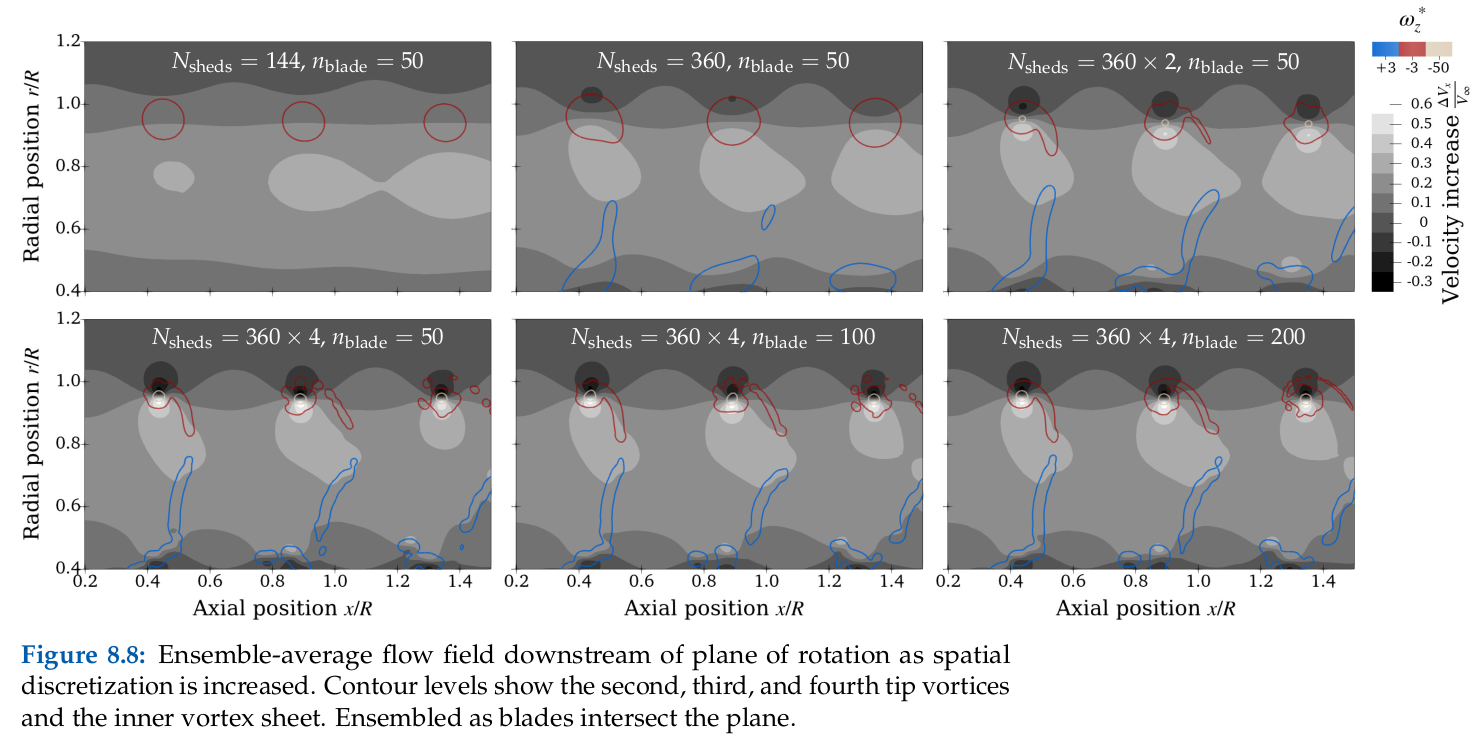
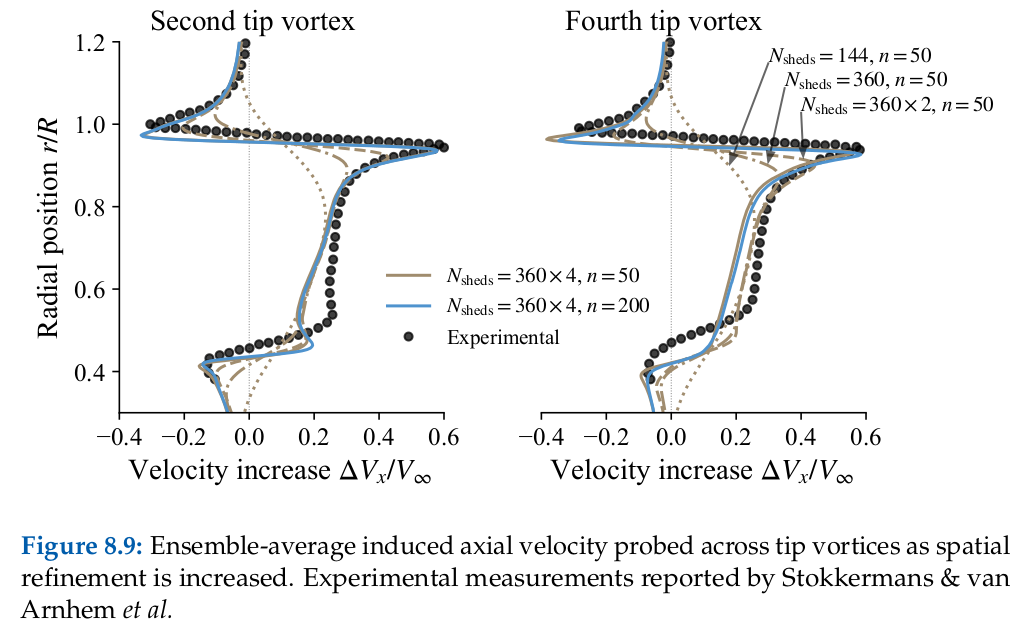
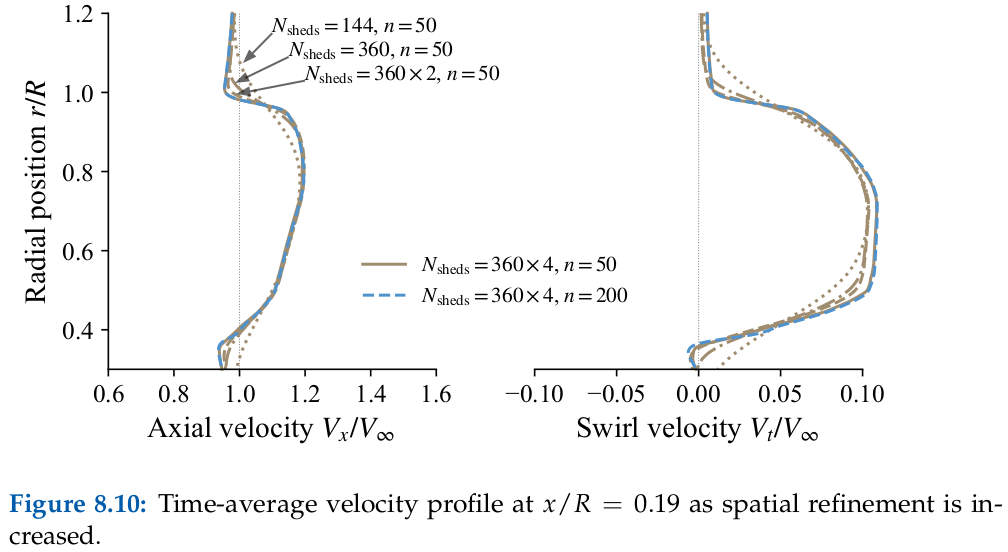
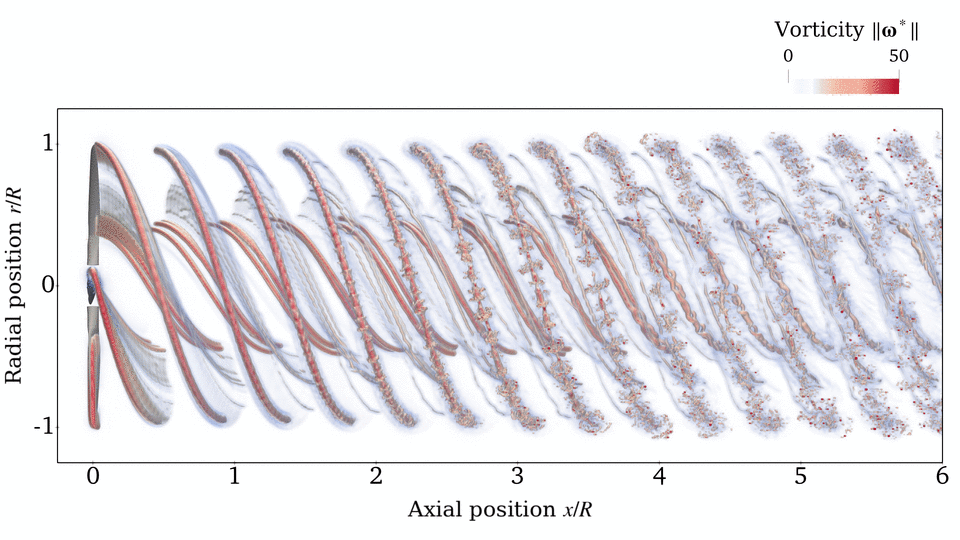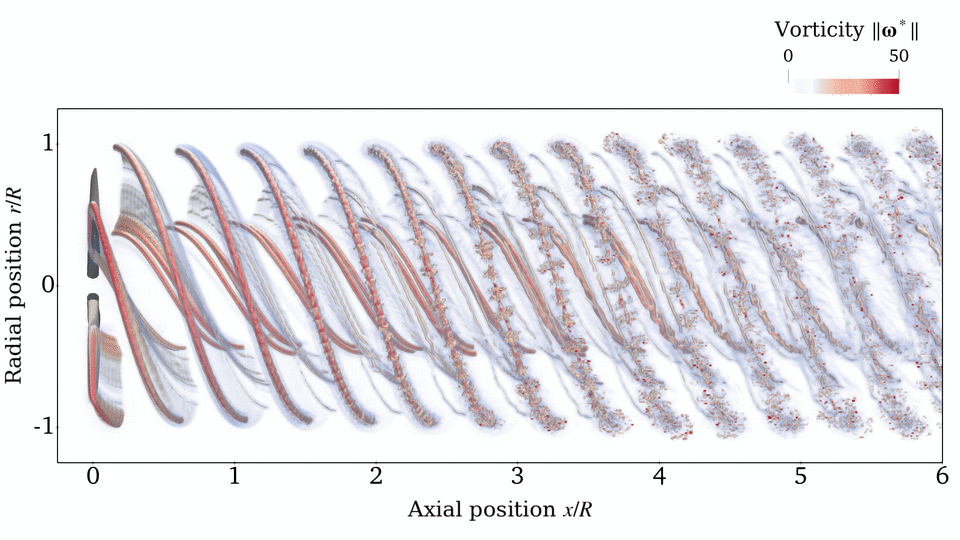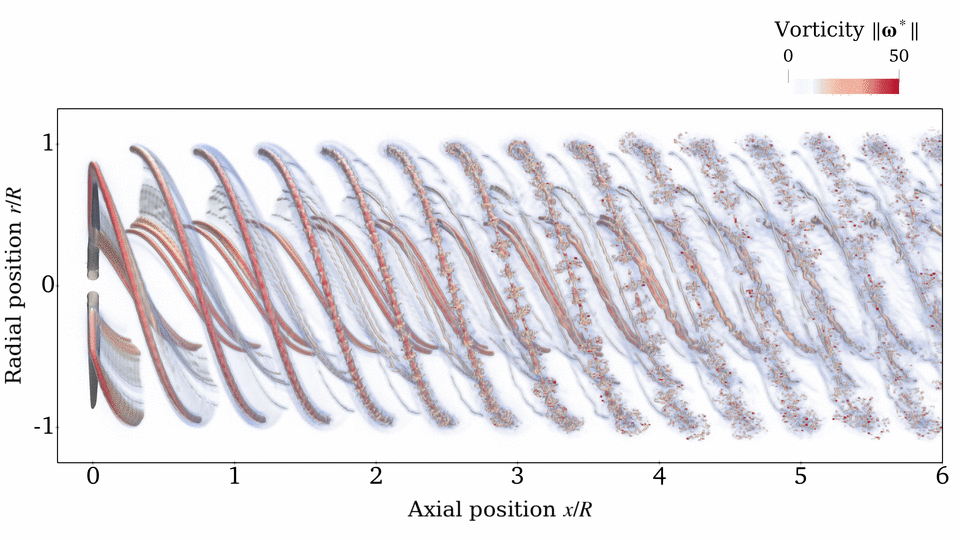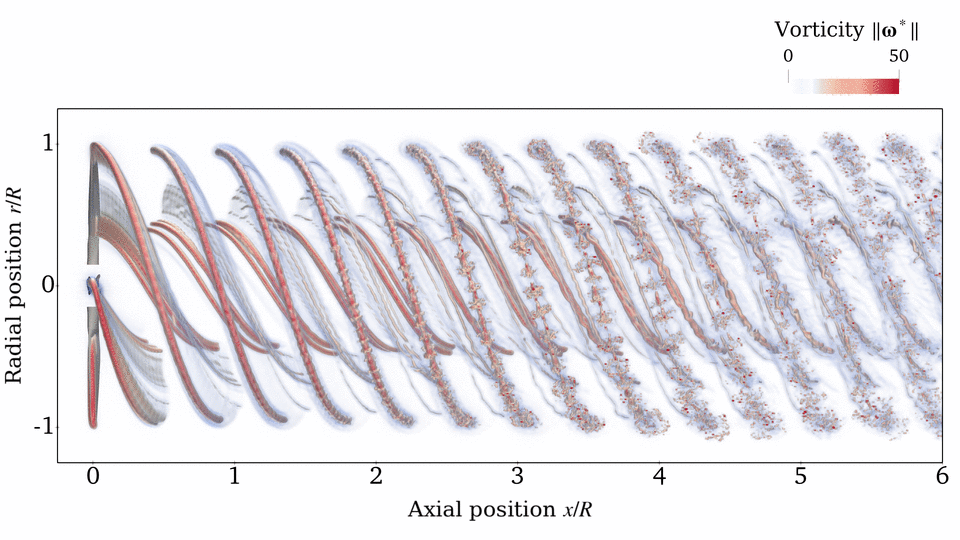
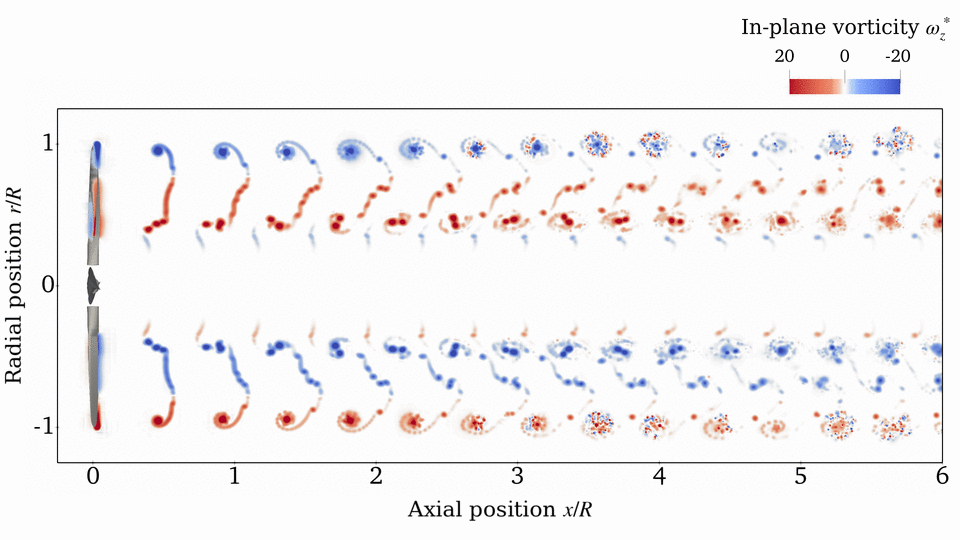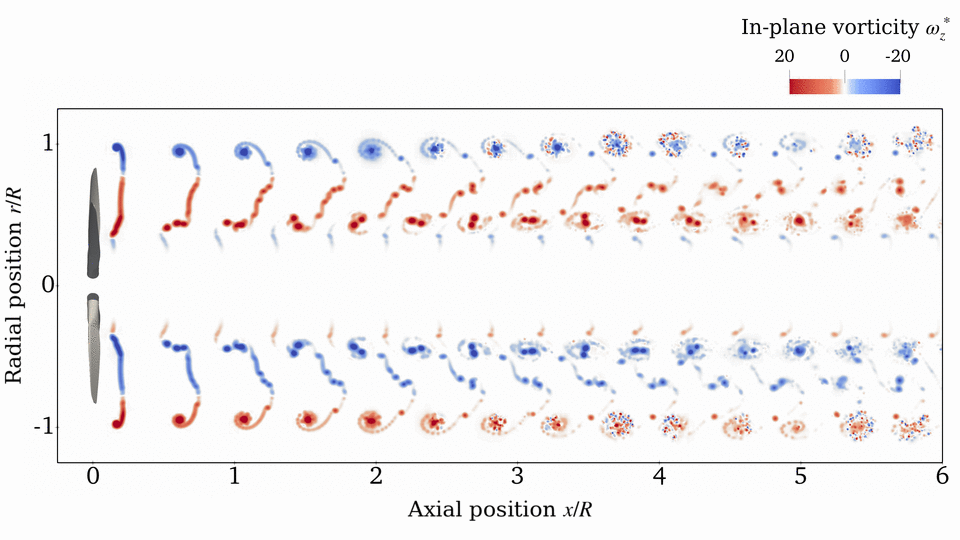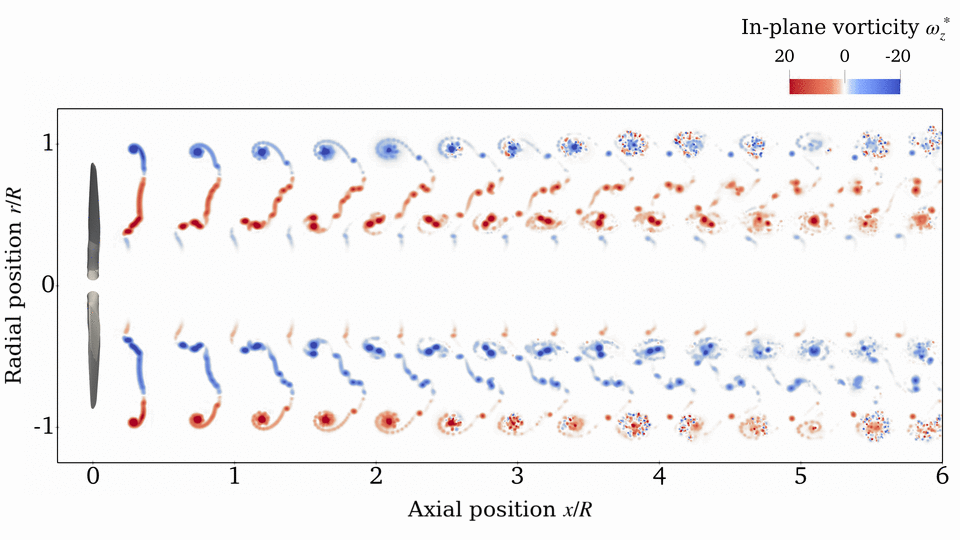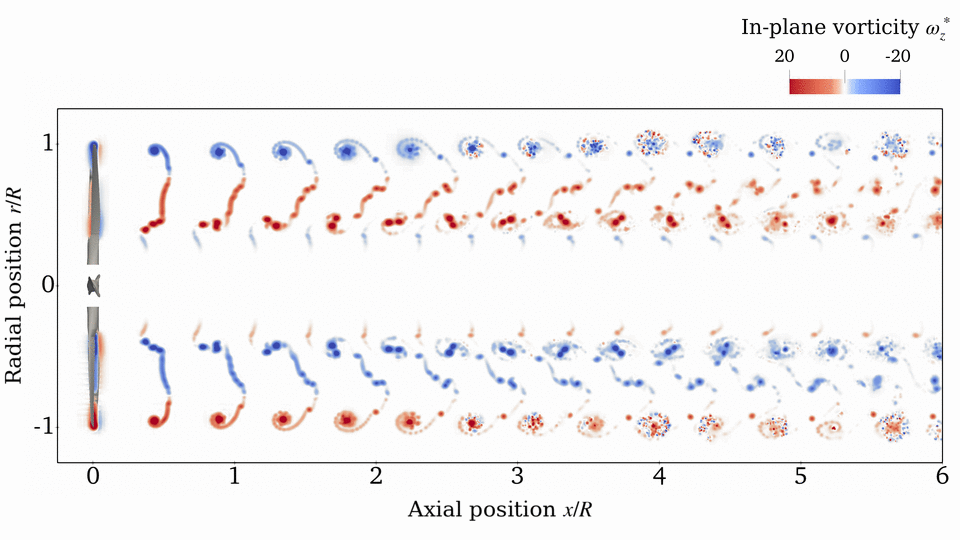
Rotor Wake
Source: E. J. Alvarez, 2022[1], and E. J. Alvarez and A. Ning, 2023[3]
Case: Continuation of Beaver propeller convergence study. Wake structure and flow field compared to experimental PIV measurements.
Takeaways: Even though the aerodynamic performance of the rotor (thrust, torque, and blade loading) is sufficiently converged with $N_\mathrm{sheds}=144$ and $n=50$, higher refinement might be needed in order to properly time-resolve the vortical structure downstream of the rotor (which might be important when the rotor wake impinges on another surface). However, $N_\mathrm{sheds}=144$ and $n=50$ is sufficient to capture the time-average velocity in the wake. This study shows that tip vortices and the inner vortex sheet can be resolved with as much granularity as desired by going to finer discretizations.
Immersed Vorticity
We have noticed that in cases with strong wake interactions (e.g., a rotor wake impinging on a wing surface), the size of the particles used to immerse the surface vorticity can change the effects of the interaction. However, over the years we have discovered a heuristic that seems to converge to the right solution, independent of the nature of the problem: the size of the embedded particles needs to be about two orders of magnitude smaller than the relevant length scale.
In FLOWUnsteady, there are three different core sizes related to the immersed vorticity:
- $\sigma_\mathrm{rotor}$, smoothing radius of the rotor bound vorticity (
sigma_rotor_surf)- $\sigma_\mathrm{LBV}$, smoothing radius of the lifting bound vorticity of wings (
sigma_vlm_surf)- $\sigma_\mathrm{TBV}$, smoothing radius of the trailing bound vorticity of wings (
vlm_vortexsheet_sigma_tbv)Accordingly, whenever possible, we recommend choosing $\sigma$-values close to
- $\sigma_\mathrm{rotor} \approx 0.01D$, where $D$ is the rotor diameter
- $\sigma_\mathrm{LBV} \approx 0.01b$, where $b$ is the wing span
- $\sigma_\mathrm{TBV} \approx 0.01t$, where $t$ is the thickness of the wing
The following is an excerpt from E. J. Alvarez, 2022,[1] Sec. 8.3., confirming the validity of the "$\sigma \approx 0.01\ell$" heuristic:

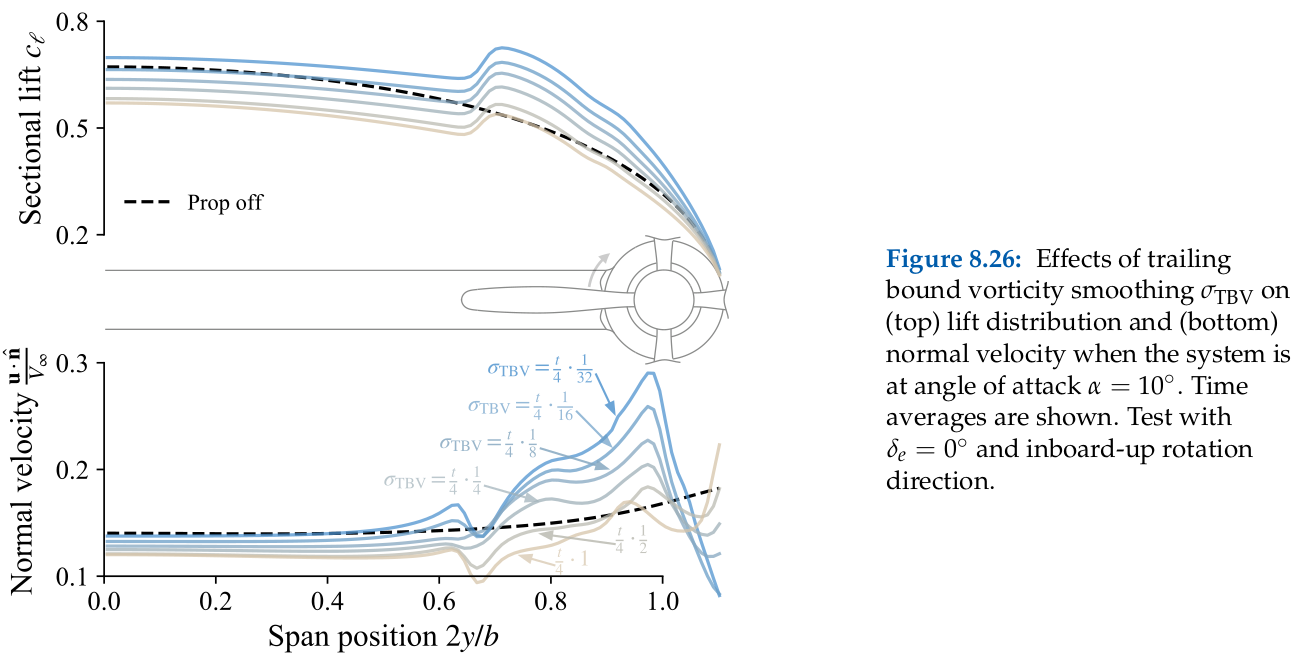



- 1E. J. Alvarez (2022), "Reformulated Vortex Particle Method and Meshless Large Eddy Simulation of Multirotor Aircraft," Doctoral Dissertation, Brigham Young University. [PDF]
- 2E. J. Alvarez & A. Ning (2020), "High-Fidelity Modeling of Multirotor Aerodynamic Interactions for Aircraft Design," AIAA Journal. [DOI] [PDF]
- 3E. J. Alvarez & A. Ning (2023), "Meshless Large Eddy Simulation of Propeller-Wing Interactions Through the Reformulated Vortex Particle Method," Journal of Aircraft. [DOI] [PDF]
- 4J. Mehr, E. J. Alvarez, & A. Ning (2022), "Interactional Aerodynamics Analysis of a Multi-Rotor Energy Kite," (in review).