AOA Sweep

Using the same vehicle, maneuver, and simulation defined in the previous section, we now run a sweep of the angle of attack.

#=##############################################################################
# DESCRIPTION
    AOA sweep on 45° swept-back wing
=###############################################################################
import FLOWUnsteady: cross, dot, norm, plt, @L_str

AOAs        = [0, 2.1, 4.2, 6.3, 8.4, 10.5, 12] # (deg) angles of attack
Xac         = [0.25*b/ar, 0, 0]             # (m) aerodynamic center for moment calculation

# Results are stored in these arrays
CLs, CDs    = [], []                        # Lift and drag at each angle of attack
rolls, pitchs, yaws = [], [], []            # Rolling, pitching, and yawing moment

ls, ds      = [], []                        # Load and drag distributions
spanposs    = []                            # Spanwise positions for load distributions


# ----------------- AOA SWEEP --------------------------------------------------
for AOA in AOAs

    println("\n\n Running AOA = $(AOA) deg")

    # ------------- RUN SIMULATION ----------------

    # Freestream function
    Vinf(X, t) = magVinf*[cosd(AOA), 0.0, sind(AOA)]

    # Define wing monitor with new reference freestream direction
    Shat = [0, 1, 0]                            # Spanwise direction
    Dhat = [cosd(AOA), 0.0, sind(AOA)]          # Direction of drag
    Lhat = cross(Dhat, Shat)                    # Direction of lift

    # Generate wing monitor
    monitor = uns.generate_monitor_wing(wing, Vinf, b, ar,
                                                rho, qinf, nsteps;
                                                calc_aerodynamicforce_fun=calc_aerodynamicforce_fun,
                                                L_dir=Lhat,
                                                D_dir=Dhat,
                                                save_path=nothing,
                                                disp_plot=false
                                                )

    # Run simulation
    pfield = uns.run_simulation(simulation, nsteps;
                                    # SIMULATION OPTIONS
                                    Vinf=Vinf,
                                    rho=rho,
                                    # SOLVERS OPTIONS
                                    p_per_step=p_per_step,
                                    max_particles=max_particles,
                                    sigma_vlm_solver=sigma_vlm_solver,
                                    sigma_vlm_surf=sigma_vlm_surf,
                                    sigma_rotor_surf=sigma_vlm_surf,
                                    sigma_vpm_overwrite=sigma_vpm_overwrite,
                                    shed_starting=shed_starting,
                                    extra_runtime_function=monitor,
                                    # OUTPUT OPTIONS
                                    save_path=nothing,
                                    v_lvl=1, verbose_nsteps=60
                                    )

    # ------------- POST-PROCESSING ---------------

    # Integrate total lift and drag
    L = sum(wing.sol["L"])
    D = sum(wing.sol["D"])

    # Lift and drag coefficients
    CL = norm(L) / (qinf*b^2/ar)
    CD = norm(D) / (qinf*b^2/ar)

    # Control point of each element
    Xs = [vlm.getControlPoint(wing, i) for i in 1:vlm.get_m(wing)]

    # Force of each element
    Fs = wing.sol["Ftot"]

    # Integrate the total moment with respect to aerodynamic center
    M = sum( cross(X - Xac, F) for (X, F) in zip(Xs, Fs) )

    # Integrated moment decomposed into rolling, pitching, and yawing moments
    lhat = Dhat                   # Rolling direction
    mhat = Shat                   # Pitching direction
    nhat = Lhat                   # Yawing direction

    roll = dot(M, lhat)
    pitch = dot(M, mhat)
    yaw = dot(M, nhat)

    # Sectional loading (in vector form) at each control point
    fs = wing.sol["ftot"]

    # Decompose vectors into lift and drag distribution
    l = [ dot(f, Lhat) for f in fs ]
    d = [ dot(f, Dhat) for f in fs ]

    # Span position of each control point
    spanpos = [ dot(X, Shat) / (b/2) for X in Xs ]

    # Store results
    push!(CLs, CL)
    push!(CDs, CD)

    push!(rolls, roll)
    push!(pitchs, pitch)
    push!(yaws, yaw)

    push!(spanposs, spanpos)
    push!(ls, l)
    push!(ds, d)

end

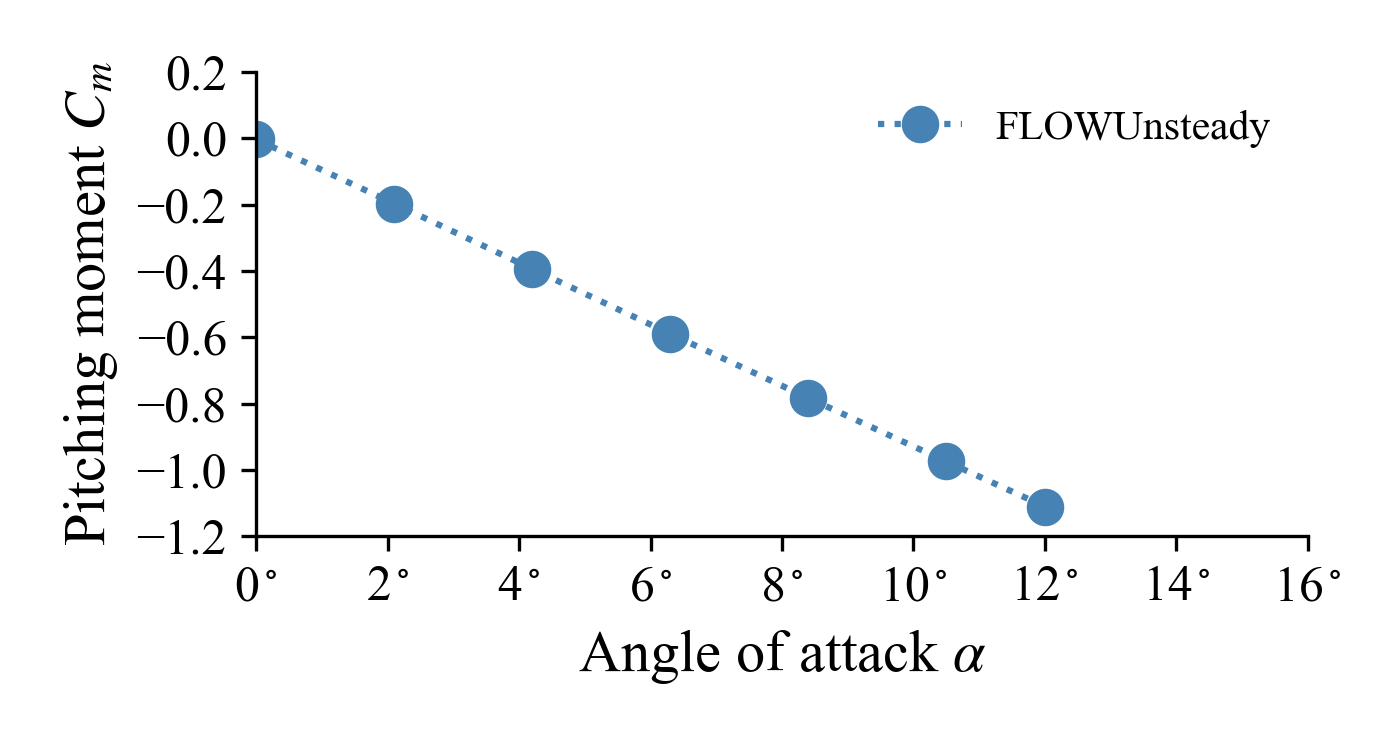
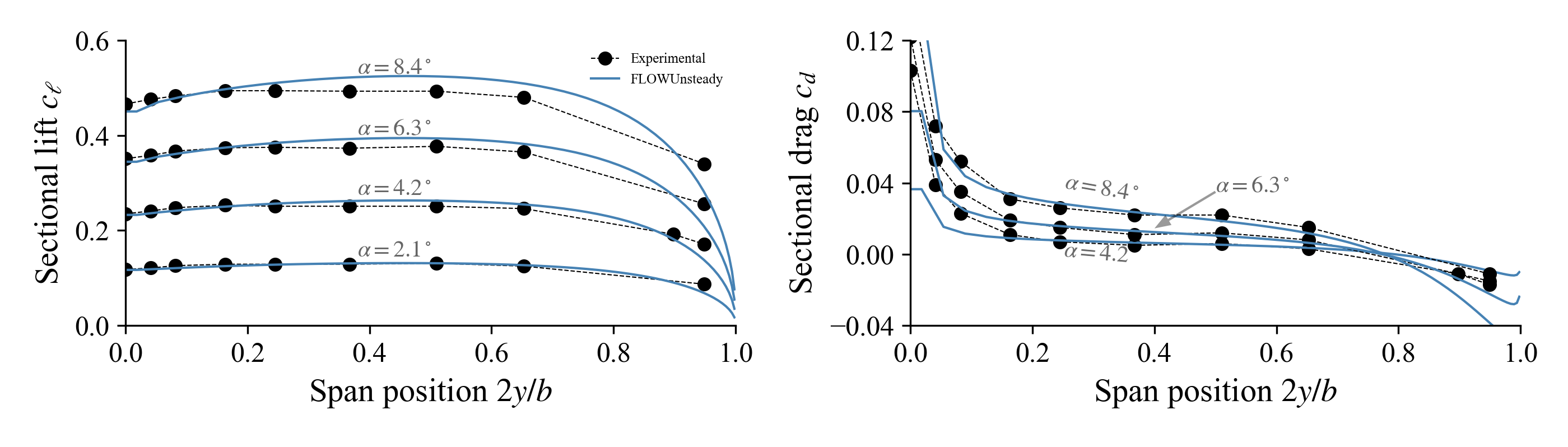
Check examples/wing/wing_aoasweep.jl to see how to postprocess and plot the results as shown below.

Spanwise loading distribution

Vehicle lift and drag

Pitching moment