Maneuver Definition
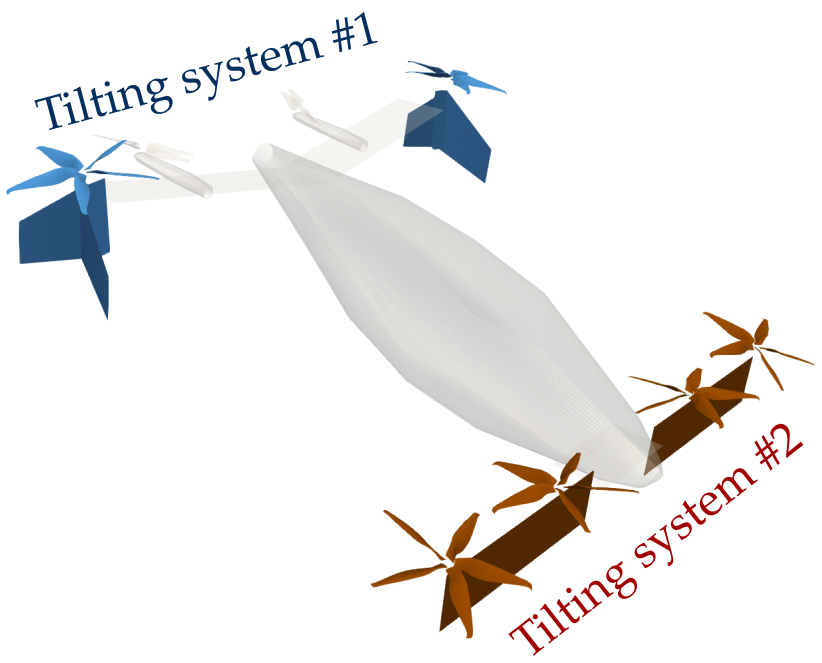
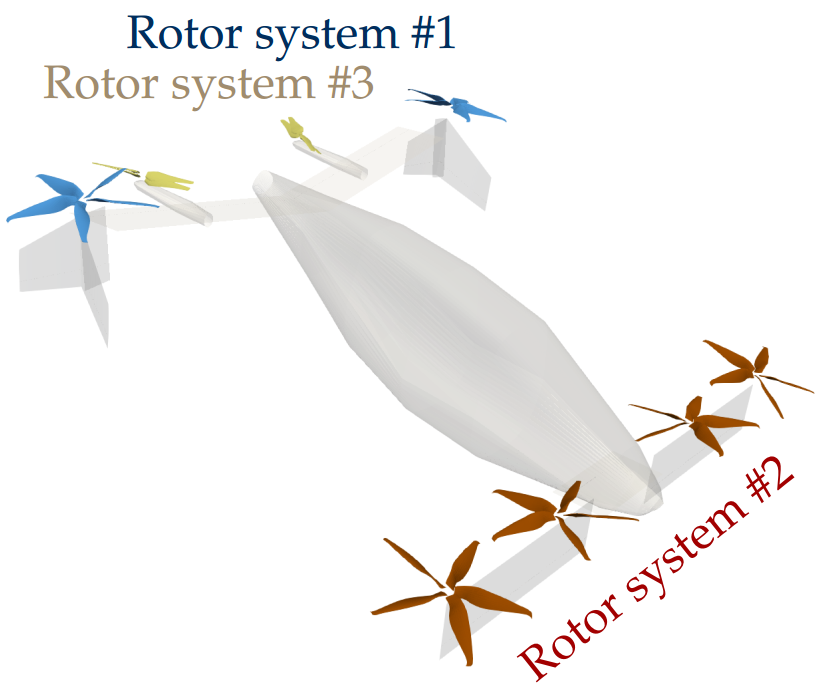
In this section we define a function that generates the eVTOL transition maneuver (a uns.KinematicManeuver object). This maneuver object contains the non-dimensional velocity and attitude of the aircraft over a non-dimensional time (where $t=0$ is the beginning of the maneuver and $t=1$ is the end), which prescribes the kinematics of the vehicle. It also contains the control inputs for the aircraft over time: tilting angles for each tilting system and RPM for each rotor system shown below.
|
|
The maneuver here defined contains five stages:
- Takeoff, climb, hover
- Hover $\rightarrow$ cruise transition (powered lift to wing-borne flight)
- Cruise
- Cruise $\rightarrow$ hover transition (wing-borne flight to powered lift)
- Hover, descend, landing
Since the vehicle kinematics and control inputs used in the maneuver definition are non-dimensional, the maneuver can be performed as fast or as slow as desired when we define the total time, reference velocity, and reference RPM of uns.Simulation later in the next section, without needing to change the maneuver definition shown here.
"""
Generates the eVTOL transition maneuver of Vahana aircraft
"""
function generate_maneuver_vahana(; disp_plot=false, # If true, it will display a plot of the maneuver
add_rotors=true, # Whether to add rotors contorl inputs to the maneuver
V0=0.0001 # Initial non-dimensional velocity (slightly different than zero to avoid instabilities)
)
# NOTE: The following parameters are non-dimensional and scaled between 0
# and 1. Here, t=0 is the beginning of the maneuver and t=1 is the end.
# Define end time of each stage
# Stage 1: [0, t1] -> Take off
# Stage 2: [t1, t2] -> Transition
# Stage 3: [t2, t3] -> Cruise
# Stage 4: [t3, t4] -> Transition
# Stage 5: [t4, 1 ] -> Landing
t1, t2, t3, t4 = 0.2, 0.3, 0.5, 0.6
# Target velocity at each stage (ratio of cruise velocity)
V1 = 0.25
V2 = 0.10
V3 = 1.00
V4 = V2
V5 = 0.5*V1
# Target RPM at each stage (ratio of hover RPM)
RPM1 = 1.10
RPM2 = 1.50
RPM3 = 0.75
RPM3_stacked = 2/600
RPM4 = 1.00
RPM5 = 0.90
r_RPMh_stup = 3.50 # Ratio between stacked and main rotor RPM in hover
r_RPMh_tw = 0.75 # Ratio between tandem and main rotor RPM in hover
# NOTE: -x is in the direction of flight and +z is climb with ground at z=0
############################################################################
# AIRCRAFT VELOCITY
############################################################################
"""
Receives a nondimensional time between 0 and 1, and returns the
non-dimensional velocity vector of the aircraft at that instant.
"""
function Vaircraft(t)
# ------------ TAKE OFF ------------------------------------------------
if t<t1
# Weibull acceleration to target climb
if t<t1/2
val = t / (t1/2)
Vz = V0 + V1*(1-exp(-(2*val)^5))
# Weibull deceleration to hover
else
val = 1 - (t-t1/2) / (t1/2)
Vz = V1*(1-exp(-(2*val)^5))
end
return [0, 0, Vz]
# ------------ TRANSITION ----------------------------------------------
elseif t<t2
# Weibull acceleration to cruise
val = 1.5 * (t-t1) / (t2-t1) + 0.25
Vx = V3*(1-exp(-(val)^5))
# Slight drop during transition
val = (1/0.8) * (t-t1) / (t2-t1)
Vz = 0.5 * (5 * val^4 * exp(-val^5))
Vz = 0.2*V3 * Vz
return [-Vx, 0, -Vz]
# ------------ CRUISE --------------------------------------------------
elseif t<t3
return [-V3, 0, 0]
# ------------ TRANSITION ----------------------------------------------
elseif t<t4
# Weibull deceleration to hover
val = 1.5 * (1 - (t-t3) / (t4-t3))
Vx = V3*(1-exp(-(val)^5))
# Slight climb during transition
val = 2.0 * (t-t3) / (t4-t3)
Vz = 0.5 * (5 * val^4 * exp(-val^5))
Vz = 0.2*V3 * Vz
return [-Vx, 0, Vz]
# ------------ LANDING -------------------------------------------------
else
# Weibull acceleration to target descend
if (t-t4)<(1-t4)*0.35
val = (t-t4) / ((1-t4)*0.35)
Vz = V5*(1-exp(-(2*val)^5))
# Weibull deceleration to hover
else
val = 1 - ((t-t4) - (1-t4)*0.35) / ((1-t4)*(1-0.35))
Vz = V0 + V5*(1-exp(-(2*val)^10))
end
return [0, 0, -Vz]
end
end
############################################################################
# AIRCRAFT ANGLES
############################################################################
"""
Receives a nondimensional time between 0 and 1, and returns the attitude
of the aircraft. The attitude is a vector indicating the angle of the
vehicle frame with respect to each global axis.
"""
function angleaircraft(t)
# ------------ TAKE OFF ------------------------------------------------
if t<t1
return [0, 0, 0]
# ------------ TRANSITION ----------------------------------------------
elseif t<t2
# Slightly pitching down during transition
val = 1.5 * (t-t1) / (t2-t1)
val3 = 1.5*val
val3 = (val3)^(val3 < 1 ? 3 : 1.5)
angle_aircraft = -15*(1.5/0.75 * val3^0.5 * exp(-(val3^1.5)))
return [0, angle_aircraft, 0]
# ------------ CRUISE --------------------------------------------------
elseif t<t3
return [0, 0, 0]
# ------------ TRANSITION ----------------------------------------------
elseif t<t4
# Weibull deceleration to hover
val = 1.5 * (1 - (t-t3) / (t4-t3))
# Slight climb during transition
val = 2.0 * (t-t3) / (t4-t3)
angle_aircraft = 15 * 0.5 * (5 * val^4 * exp(-val^5))
return [0, angle_aircraft, 0]
# ------------ LANDING -------------------------------------------------
else
return [0, 0, 0]
end
end
############################################################################
# CONTROL INPUT: TILTING SYSTEMS
############################################################################
"""
Receives a nondimensional time between 0 and 1, and returns a vector
with the angles of the main-wing system (in degrees) relative to the
aircraft frame.
This tilting system is made out of the tip-mounted tiltrotors on the
main wing and winglets.
"""
function angle_main(t)
# ------------ TAKE OFF ------------------------------------------------
if t<t1
# Tiltrotors pointing up
return [0, 90, 0]
# ------------ TRANSITION ----------------------------------------------
elseif t<t2
# Tilt forward to cruise position
val = 1.5 * (t-t1) / (t2-t1)
val2 = val - 0.00
angle = 90 - 90*(1-exp(-(val2)^6))
return [0, angle, 0]
# ------------ CRUISE --------------------------------------------------
elseif t<t3
# Tiltrotors pointing forward in propeller mode
return [0, 0, 0]
# ------------ TRANSITION ----------------------------------------------
elseif t<t4
# Tilt back to hover position
val = 1.5 * (1 - (t-t3) / (t4-t3))
angle = 90 - 90*(1-exp(-(val)^5))
return [0, angle, 0]
# ------------ LANDING -------------------------------------------------
else
# Tiltrotors pointing up
return [0, 90, 0]
end
end
"""
Receives a nondimensional time between 0 and 1, and returns a vector
with the angles of the tandem-wing system (in degrees) relative to the
aircraft frame.
This tilting system is made out of the tandem wing and rotors.
"""
function angle_tandem(t)
# ------------ TAKE OFF ------------------------------------------------
if t<t1
# System pointing up
return [0, 90, 0]
# ------------ TRANSITION ----------------------------------------------
elseif t<t2
# Tilt forward to cruise position
val = 2.0 * (t-t1) / (t2-t1)
val1 = val + 0.25
angle = 90 - 90*(1-exp(-(val1)^5))
return [0, angle, 0]
# ------------ CRUISE --------------------------------------------------
elseif t<t3
# System pointing forward in cruise mode
return [0, 0, 0]
# ------------ TRANSITION ----------------------------------------------
elseif t<t4
# Tilt back to hover position
val = 1.5 * (1 - (t-t3) / (t4-t3))
angle = 90 - 90*(1-exp(-(val)^5))
return [0, angle, 0]
# ------------ LANDING -------------------------------------------------
else
# System pointing up
return [0, 90, 0]
end
end
############################################################################
# ROTORS RPM
############################################################################
"""
Receives a nondimensional time between 0 and 1, and returns the RPM of
main-wing tiltrotors normalized by the hover RPM.
"""
function RPM_main(t)
# ------------ TAKE OFF ------------------------------------------------
if t<t1
# Weibull acceleration to target climb
if t<t1/2
val = t / (t1/2)
RPM_w = RPM1*(1.05-exp(-(5*val)^2))
# Weibull deceleration to hover
else
val = 1 - (t-t1/2) / (t1/2)
RPM_w = 1.0 + (RPM1-1.0)*(1-exp(-(2*val)^5))
end
return RPM_w
# ------------ TRANSITION ----------------------------------------------
elseif t<t2
# Increase RPM to sustain forward flight and hover
if (t-t1)<(t2-t1)*0.25
val = (t-t1)/((t2-t1)*0.25)
RPM_w = 1.0 + (RPM2-1.0)*(1-exp(-(2*val)^5))
# Decrease RPM as tiltrotors transition to propeller mode
else
val = 1 - ((t2-t)/(t2-t1)-0.25) / (1-0.25)
RPM_w = RPM2 + (RPM3-RPM2)*(1-exp(-(1.1*val)^5))
end
return RPM_w
# ------------ CRUISE --------------------------------------------------
elseif t<t3
# Propeller mode
RPM_w = RPM3
return RPM_w
# ------------ TRANSITION ----------------------------------------------
elseif t<t4
# Weibull acceleration to hover
val = 1.5 * (1 - (t-t3) / (t4-t3))
RPM_w = RPM4 + (RPM3-RPM4)*(1-exp(-(val)^3))
return RPM_w
# ------------ LANDING -------------------------------------------------
else
# Weibull deceleration to target descend
if (t-t4)<(1-t4)*0.55
val = (t-t4) / ((1-t4)*0.55)
RPM_w = RPM4 + (RPM5-RPM4)*(1-exp(-(3*val)^5))
# Weibull acceleration to hover
else
val = ((t-t4) - (1-t4)*0.55) / ((1-t4)*(1-0.55))
val = val + 0.60
RPM_w = RPM5*(3.0*(val)^(3.0-1)*exp(-(val)^5.0))/1.0
end
return RPM_w
end
end
"""
Receives a nondimensional time between 0 and 1, and returns the RPM of
stacked upper rotors in main wing normalized by the hover RPM.
"""
function RPM_stacked_up(t)
# ------------ TAKE OFF ------------------------------------------------
if t<t1
# Weibull acceleration to target climb
if t<t1/5
val = t / (t1/5)
RPM_w = RPM1*(1.05-exp(-(5*val)^2))
# Weibull deceleration to hover
else
val = 1 - (t-t1/5) / (1-t1/5)
RPM_w = 1.0 + (RPM1-1.0)*(1-exp(-(2*val)^5))
end
return r_RPMh_stup*RPM_w
# ------------ TRANSITION ----------------------------------------------
elseif t<t2
# Increase RPM to sustain forward flight and hover
if (t-t1)<(t2-t1)*0.65
val = (t-t1)/((t2-t1)*0.65)
RPM_tw = r_RPMh_tw*(1.0 + (RPM2-1.0)*(1-exp(-(2*val)^5)))
# Decrease RPM as it transitions out of powered lift
else
val = 1 - (t2-t)/(t2-((t2-t1)*0.65 + t1))
RPM_tw = r_RPMh_tw*(RPM2 + val*(RPM3_stacked-RPM2))
end
return RPM_tw
# ------------ CRUISE --------------------------------------------------
elseif t<t3
# Stopped rotor
return RPM3_stacked
# ------------ TRANSITION ----------------------------------------------
elseif t<t4
# Weibull acceleration to hover
val = 1.5 * (1 - (t-t3) / (t4-t3))
RPM_w = RPM4 + (RPM3_stacked-RPM4)*(1-exp(-(val)^3))
return r_RPMh_stup*RPM_w
# ------------ LANDING -------------------------------------------------
else
# Weibull deceleration to target descend
if (t-t4)<(1-t4)*0.75
val = (t-t4) / ((1-t4)*0.75)
RPM_w = RPM4 + (RPM5-RPM4)*(1-exp(-(3*val)^5))
# Weibull acceleration to hover
else
val = ((t-t4) - (1-t4)*0.75) / ((1-t4)*(1-0.75))
val = val + 0.60
RPM_w = RPM5*(3.0*(val)^(3.0-1)*exp(-(val)^5.0))/1.0
end
return r_RPMh_stup*RPM_w
end
end
"""
Receives a nondimensional time between 0 and 1, and returns the RPM of
stacked lower rotors in main wing normalized by the hover RPM.
"""
function RPM_stacked_low(t)
# ------------ TAKE OFF ------------------------------------------------
if t<t1
return RPM_stacked_up(t)
# ------------ TRANSITION ----------------------------------------------
elseif t<t2
return RPM_stacked_up(t)
# ------------ CRUISE --------------------------------------------------
elseif t<t3
return RPM_stacked_up(t)
# ------------ TRANSITION ----------------------------------------------
elseif t<t4
return RPM_stacked_up(t)
# ------------ LANDING -------------------------------------------------
else
return RPM_stacked_up(t)
end
end
"""
Receives a nondimensional time between 0 and 1, and returns the RPM of
tandem wing rotors normalized by the hover RPM.
"""
function RPM_tandem(t)
# ------------ TAKE OFF ------------------------------------------------
if t<t1
return r_RPMh_tw*RPM_main(t)
# ------------ TRANSITION ----------------------------------------------
elseif t<t2
# Increases RPM to sustain forward flight and hover
if (t-t1)<(t2-t1)*0.65
val = (t-t1)/((t2-t1)*0.65)
RPM_tw = r_RPMh_tw*(1.0 + (RPM2-1.0)*(1-exp(-(2*val)^5)))
# Decrease RPM as rotors transition to propeller mode
else
val = 1 - (t2-t)/(t2-((t2-t1)*0.65 + t1))
RPM_tw = r_RPMh_tw*(RPM2 + val*(RPM3-RPM2))
end
return RPM_tw
# ------------ CRUISE --------------------------------------------------
elseif t<t3
return r_RPMh_tw*RPM_main(t)
# ------------ TRANSITION ----------------------------------------------
elseif t<t4
# Weibull acceleration to hover
val = 1.5 * (1 - (t-t3) / (t4-t3))
RPM_tw = r_RPMh_tw * (RPM4 + (RPM3-RPM4)*(1-exp(-(0.8*val)^8)))
return RPM_tw
# ------------ LANDING -------------------------------------------------
else
return r_RPMh_tw*RPM_main(t)
end
end
############################################################################
# MANEUVER OBJECT
############################################################################
# Angle function of each tilting system
angle = (angle_main, angle_tandem)
# RPM function of each rotor system
if add_rotors
RPM = (RPM_main, RPM_stacked_up, RPM_stacked_low, RPM_tandem)
else
RPM = ()
end
# Aircraft velocity and angles (attitude)
Vvehicle = Vaircraft
anglevehicle = angleaircraft
# Define non-dimensional maneuver
maneuver = uns.KinematicManeuver(angle, RPM, Vvehicle, anglevehicle)
# Plot maneuver for verification purposes
if disp_plot
uns.plot_maneuver(maneuver; tstages=[t1, t2, t3, t4])
end
return maneuver
end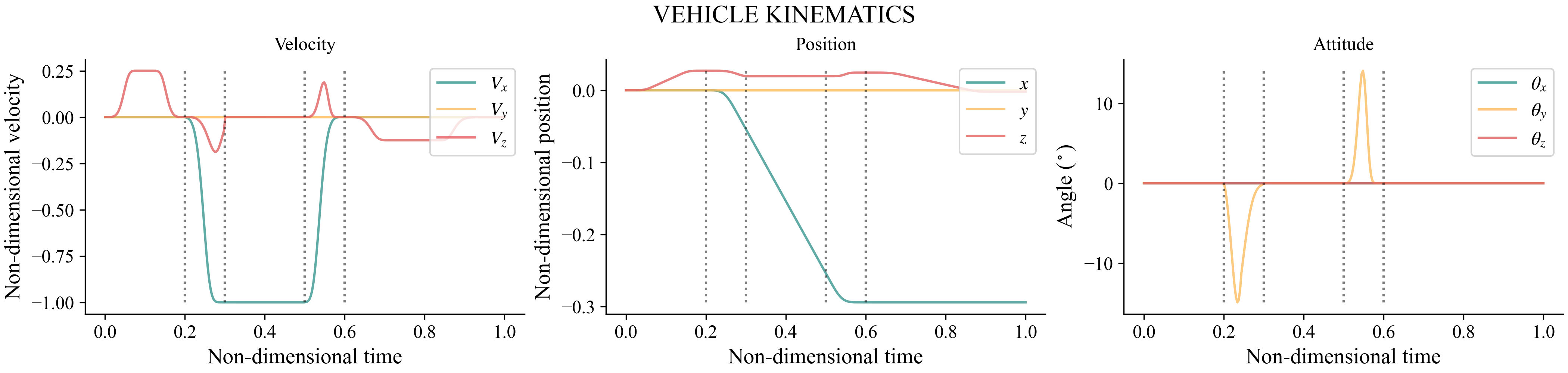
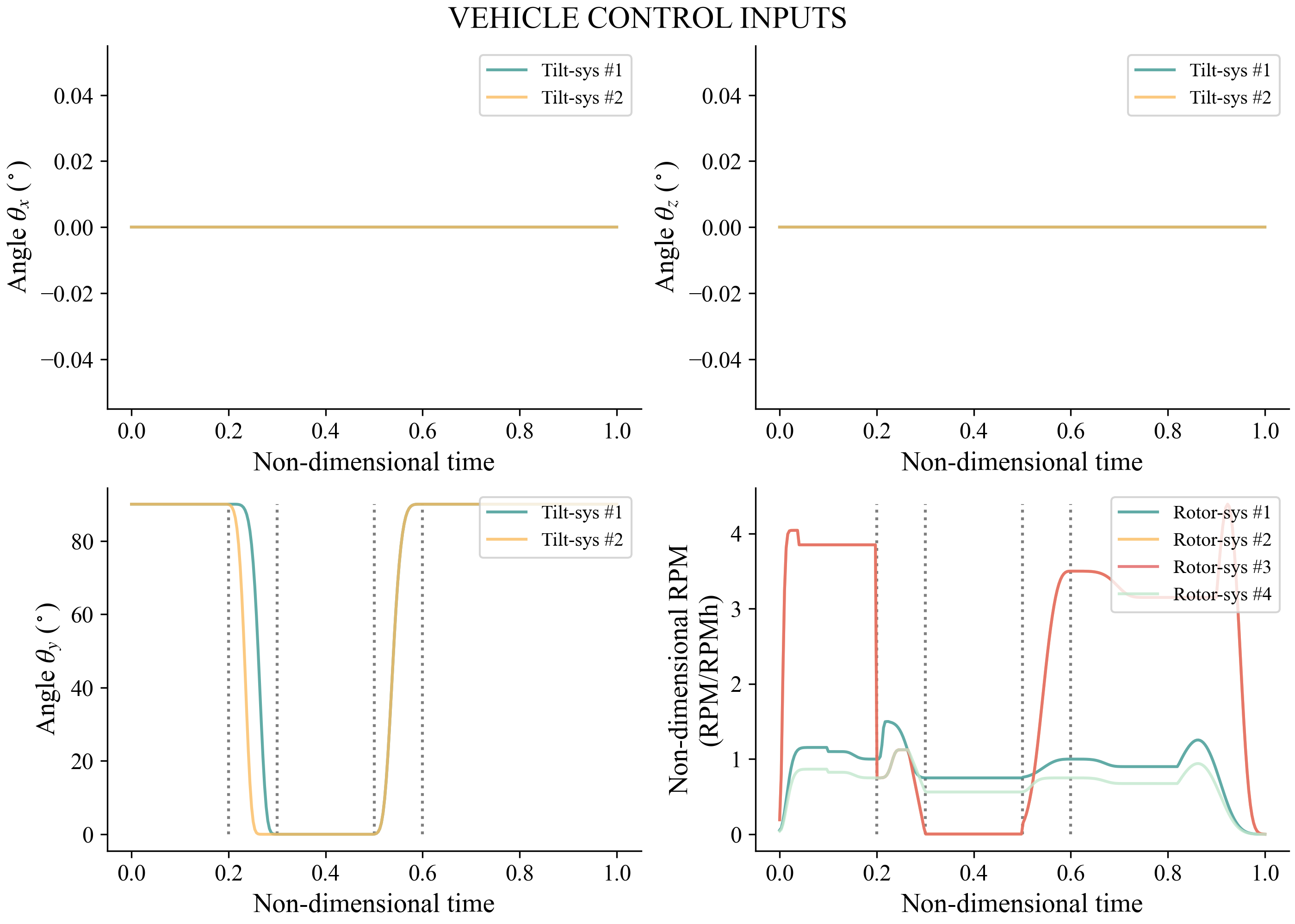
Notice that this plot shows four rotor systems instead of only three. This is because the system of stacked rotors was split into two (all upper stack rotors are grouped together, while all lower stack rotors are also grouped together). This way we could change the index angle of the stacked rotors throughout the simulation by modulating upper and lower RPMs independently. However, for simplicity, in this example we have kept upper and lower RPMs the same.