$J$ Sweep

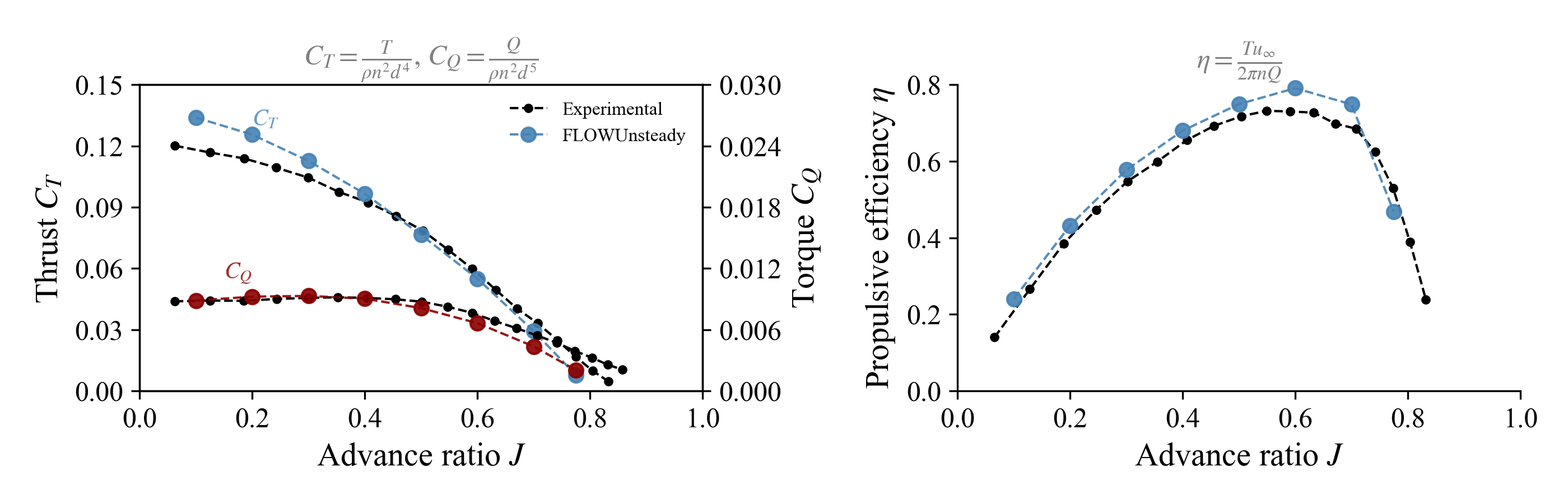
Using the same rotor from the previous section, we now run a sweep of the advance ratio $J = \frac{u_\infty}{n d}$ to characterize the performance of the propeller.

#=##############################################################################
# DESCRIPTION
    Advance ratio sweep on APC 10 x7 propeller
=###############################################################################

case_name       = "propeller-Jsweep-example"# Name of this sweep case
save_path       = case_name                 # Where to save this sweep

Js              = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.775] # Advance ratios Vinf/(nD)

# Create path where to save sweep
uns.gt.create_path(save_path, true)

# ----------------- J SWEEP ----------------------------------------------------
for J in Js

    println("\n\n Running J = $(J)")

    magVinf         = J*RPM/60*(2*R)
    Vinf(X, t)      = magVinf*[cosd(AOA), sind(AOA), 0] # (m/s) freestream velocity vector

    # ------------- 1) VEHICLE DEFINITION ---------
    println("\tGenerating geometry...")

    # Generate rotor
    rotor = uns.generate_rotor(rotor_file; pitch=pitch,
                                            n=n, CW=CW, blade_r=r,
                                            altReD=[RPM, J, mu/rho],
                                            xfoil=xfoil,
                                            ncrit=ncrit,
                                            data_path=data_path,
                                            verbose=false,
                                            verbose_xfoil=false,
                                            plot_disc=false
                                            );


    # Generate vehicle
    system = vlm.WingSystem()                   # System of all FLOWVLM objects
    vlm.addwing(system, "Rotor", rotor)

    rotors = [rotor];                           # Defining this rotor as its own system
    rotor_systems = (rotors, );                 # All systems of rotors

    wake_system = vlm.WingSystem()              # System that will shed a VPM wake
                                                # NOTE: Do NOT include rotor when using the quasi-steady solver
    if VehicleType != uns.QVLMVehicle
        vlm.addwing(wake_system, "Rotor", rotor)
    end

    vehicle = VehicleType(  system;
                            rotor_systems=rotor_systems,
                            wake_system=wake_system
                            );

    # ------------- 2) MANEUVER DEFINITION --------
    # No changes

    # ------------- 3) SIMULATION DEFINITION ------
    simulation = uns.Simulation(vehicle, maneuver, Vref, RPMref, ttot;
                                                     Vinit=Vinit, Winit=Winit);

    # ------------- 4) MONITOR DEFINITION ---------
    monitor_rotor = uns.generate_monitor_rotors(rotors, J, rho, RPM, nsteps;
                                                t_scale=RPM/60,
                                                t_lbl="Revolutions",
                                                save_path=save_path,
                                                run_name="J$(ceil(Int, J*100))",
                                                disp_conv=false,
                                                figname="rotor monitor J=$(J)",
                                                )

    # ------------- 5) RUN SIMULATION -------------
    println("\tRunning simulation...")

    uns.run_simulation(simulation, nsteps;
                        # ----- SIMULATION OPTIONS -------------
                        Vinf=Vinf,
                        rho=rho, mu=mu, sound_spd=speedofsound,
                        # ----- SOLVERS OPTIONS ----------------
                        p_per_step=p_per_step,
                        max_particles=max_particles,
                        vpm_viscous=vpm_viscous,
                        sigma_vlm_surf=sigma_rotor_surf,
                        sigma_rotor_surf=sigma_rotor_surf,
                        sigma_vpm_overwrite=sigma_vpm_overwrite,
                        vlm_rlx=vlm_rlx,
                        shed_unsteady=shed_unsteady,
                        shed_starting=shed_starting,
                        extra_runtime_function=monitor_rotor,
                        # ----- OUTPUT OPTIONS ------------------
                        save_path=nothing,
                        v_lvl=1, verbose_nsteps=24
                        );
end

Check examples/propeller/propeller_jsweep.jl to postprocess and plot the results as shown below.