Basics

In this example we first simulate an APC Thin-Electric 10x7 propeller operating in cruise conditions. Along the way, we demonstrate the basics of how to set up and run a rotor simulation.
Rotors are generated through the function FLOWUnsteady.generate_rotor, which can receive either a set of parameters that define the rotor geometry (like twist/chord/sweep distributions, etc), or it can read the rotor geometry from a file. FLOWunsteady provides a prepopulated database of airfoil and rotor geometries to automate the generation of rotors, which is found under database/. This database can be accessed through the variable FLOWUnsteady.default_database. Alternatively, users can define their own database with custom rotors and airfoils.
The following slides describe the structure of the database, using a DJI rotor as an example:
In this simulation we exemplify the following:
- How to generate a rotor with
uns.generate_rotor - How to generate a rotor monitor with
uns.generate_monitor_rotors - How to set up and run a rotor simulation.
#=##############################################################################
# DESCRIPTION
Simulation of an APC Thin-Electric 10x7 propeller (two-bladed rotor, 10-inch
diameter).
This example replicates the experiment and simulation described in McCrink &
Gregory (2017), "Blade Element Momentum Modeling of Low-Reynolds Electric
Propulsion Systems."
# AUTHORSHIP
* Author : Eduardo J. Alvarez (edoalvarez.com)
* Email : Edo.AlvarezR@gmail.com
* Created : Mar 2023
* Last updated : Mar 2023
* License : MIT
=###############################################################################
import FLOWUnsteady as uns
import FLOWVLM as vlm
import FLOWVPM as vpm
run_name = "propeller-example" # Name of this simulation
save_path = run_name # Where to save this simulation
paraview = true # Whether to visualize with Paraview
# ----------------- GEOMETRY PARAMETERS ----------------------------------------
# Rotor geometry
rotor_file = "apc10x7.csv" # Rotor geometry
data_path = uns.def_data_path # Path to rotor database
pitch = 0.0 # (deg) collective pitch of blades
CW = false # Clock-wise rotation
xfoil = true # Whether to run XFOIL
ncrit = 9 # Turbulence criterion for XFOIL
# NOTE: If `xfoil=true`, XFOIL will be run to generate the airfoil polars used
# by blade elements before starting the simulation. XFOIL is run
# on the airfoil contours found in `rotor_file` at the corresponding
# local Reynolds and Mach numbers along the blade.
# Alternatively, the user can provide pre-computer airfoil polars using
# `xfoil=false` and pointing to polar files through `rotor_file`.
# Discretization
n = 20 # Number of blade elements per blade
r = 1/5 # Geometric expansion of elements
# NOTE: Here a geometric expansion of 1/5 means that the spacing between the
# tip elements is 1/5 of the spacing between the hub elements. Refine the
# discretization towards the blade tip like this in order to better
# resolve the tip vortex.
# Read radius of this rotor and number of blades
R, B = uns.read_rotor(rotor_file; data_path=data_path)[[1,3]]
# ----------------- SIMULATION PARAMETERS --------------------------------------
# Operating conditions
RPM = 9200 # RPM
J = 0.4 # Advance ratio Vinf/(nD)
AOA = 0 # (deg) Angle of attack (incidence angle)
rho = 1.225 # (kg/m^3) air density
mu = 1.81e-5 # (kg/ms) air dynamic viscosity
speedofsound = 342.35 # (m/s) speed of sound
magVinf = J*RPM/60*(2*R)
Vinf(X, t) = magVinf*[cosd(AOA), sind(AOA), 0] # (m/s) freestream velocity vector
ReD = 2*pi*RPM/60*R * rho/mu * 2*R # Diameter-based Reynolds number
Matip = 2*pi*RPM/60*R / speedofsound # Tip Mach number
println("""
RPM: $(RPM)
Vinf: $(Vinf(zeros(3), 0)) m/s
Matip: $(round(Matip, digits=3))
ReD: $(round(ReD, digits=0))
""")
# ----------------- SOLVER PARAMETERS ------------------------------------------
# Aerodynamic solver
VehicleType = uns.UVLMVehicle # Unsteady solver
# VehicleType = uns.QVLMVehicle # Quasi-steady solver
const_solution = VehicleType==uns.QVLMVehicle # Whether to assume that the
# solution is constant or not
# Time parameters
nrevs = 4 # Number of revolutions in simulation
nsteps_per_rev = 36 # Time steps per revolution
nsteps = const_solution ? 2 : nrevs*nsteps_per_rev # Number of time steps
ttot = nsteps/nsteps_per_rev / (RPM/60) # (s) total simulation time
# VPM particle shedding
p_per_step = 2 # Sheds per time step
shed_starting = true # Whether to shed starting vortex
shed_unsteady = true # Whether to shed vorticity from unsteady loading
max_particles = ((2*n+1)*B)*nsteps*p_per_step + 1 # Maximum number of particles
# Regularization
sigma_rotor_surf= R/40 # Rotor-on-VPM smoothing radius
lambda_vpm = 2.125 # VPM core overlap
# VPM smoothing radius
sigma_vpm_overwrite = lambda_vpm * 2*pi*R/(nsteps_per_rev*p_per_step)
# Rotor solver
vlm_rlx = 0.7 # VLM relaxation <-- this also applied to rotors
hubtiploss_correction = vlm.hubtiploss_nocorrection # Hub and tip loss correction
# VPM solver
vpm_viscous = vpm.Inviscid() # VPM viscous diffusion scheme
# NOTE: In most practical situations, open rotors operate at a Reynolds number
# high enough that viscous diffusion in the wake is negligible.
# Hence, it does not make much of a difference whether we run the
# simulation with viscous diffusion enabled or not.
if VehicleType == uns.QVLMVehicle
# NOTE: If the quasi-steady solver is used, this mutes warnings regarding
# potential colinear vortex filaments. This is needed since the
# quasi-steady solver will probe induced velocities at the lifting
# line of the blade
uns.vlm.VLMSolver._mute_warning(true)
end
# ----------------- 1) VEHICLE DEFINITION --------------------------------------
println("Generating geometry...")
# Generate rotor
rotor = uns.generate_rotor(rotor_file; pitch=pitch,
n=n, CW=CW, blade_r=r,
altReD=[RPM, J, mu/rho],
xfoil=xfoil,
ncrit=ncrit,
data_path=data_path,
verbose=true,
verbose_xfoil=false,
plot_disc=true
);
println("Generating vehicle...")
# Generate vehicle
system = vlm.WingSystem() # System of all FLOWVLM objects
vlm.addwing(system, "Rotor", rotor)
rotors = [rotor]; # Defining this rotor as its own system
rotor_systems = (rotors, ); # All systems of rotors
wake_system = vlm.WingSystem() # System that will shed a VPM wake
# NOTE: Do NOT include rotor when using the quasi-steady solver
if VehicleType != uns.QVLMVehicle
vlm.addwing(wake_system, "Rotor", rotor)
end
vehicle = VehicleType( system;
rotor_systems=rotor_systems,
wake_system=wake_system
);
# NOTE: Through the `rotor_systems` keyword argument to `uns.VLMVehicle` we
# have declared any systems (groups) of rotors that share a common RPM.
# We will later declare the control inputs to each rotor system when we
# define the `uns.KinematicManeuver`.
# ------------- 2) MANEUVER DEFINITION -----------------------------------------
# Non-dimensional translational velocity of vehicle over time
Vvehicle(t) = zeros(3)
# Angle of the vehicle over time
anglevehicle(t) = zeros(3)
# RPM control input over time (RPM over `RPMref`)
RPMcontrol(t) = 1.0
angles = () # Angle of each tilting system (none)
RPMs = (RPMcontrol, ) # RPM of each rotor system
maneuver = uns.KinematicManeuver(angles, RPMs, Vvehicle, anglevehicle)
# NOTE: `FLOWUnsteady.KinematicManeuver` defines a maneuver with prescribed
# kinematics. `Vvehicle` defines the velocity of the vehicle (a vector)
# over time. `anglevehicle` defines the attitude of the vehicle over time.
# `angle` defines the tilting angle of each tilting system over time.
# `RPM` defines the RPM of each rotor system over time.
# Each of these functions receives a nondimensional time `t`, which is the
# simulation time normalized by the total time `ttot`, from 0 to
# 1, beginning to end of simulation. They all return a nondimensional
# output that is then scaled by either a reference velocity (`Vref`) or
# a reference RPM (`RPMref`). Defining the kinematics and controls of the
# maneuver in this way allows the user to have more control over how fast
# to perform the maneuver, since the total time, reference velocity and
# RPM are then defined in the simulation parameters shown below.
# ------------- 3) SIMULATION DEFINITION ---------------------------------------
Vref = 0.0 # Reference velocity to scale maneuver by
RPMref = RPM # Reference RPM to scale maneuver by
Vinit = Vref*Vvehicle(0) # Initial vehicle velocity
Winit = pi/180*(anglevehicle(1e-6) - anglevehicle(0))/(1e-6*ttot) # Initial angular velocity
simulation = uns.Simulation(vehicle, maneuver, Vref, RPMref, ttot;
Vinit=Vinit, Winit=Winit);
# ------------- 4) MONITORS DEFINITIONS ----------------------------------------
figs, figaxs = [], [] # Figures generated by monitor
# Generate rotor monitor
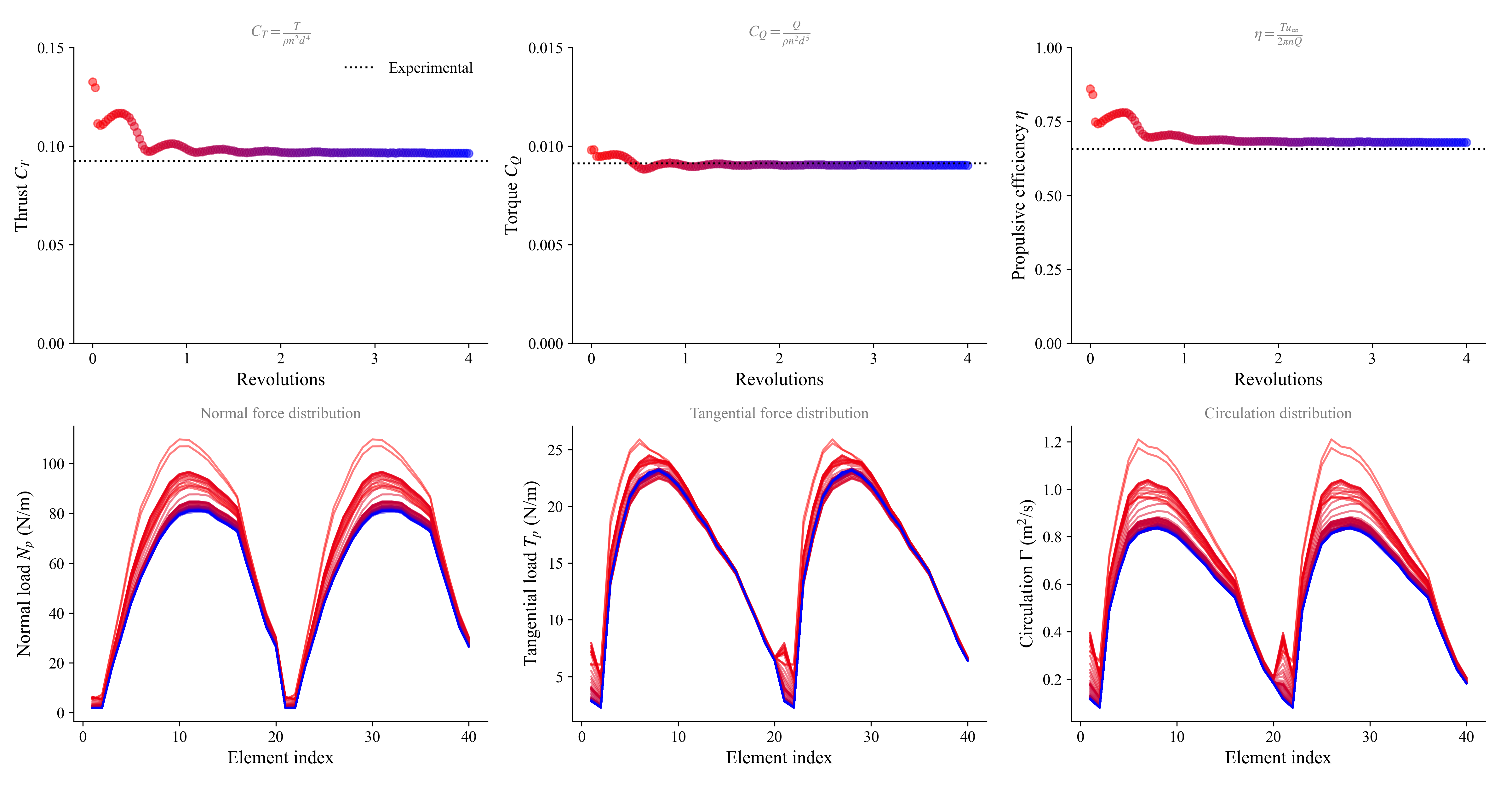
monitor_rotor = uns.generate_monitor_rotors(rotors, J, rho, RPM, nsteps;
t_scale=RPM/60, # Scaling factor for time in plots
t_lbl="Revolutions", # Label for time axis
out_figs=figs,
out_figaxs=figaxs,
save_path=save_path,
run_name=run_name,
figname="rotor monitor",
)
# ------------- 5) RUN SIMULATION ----------------------------------------------
println("Running simulation...")
uns.run_simulation(simulation, nsteps;
# ----- SIMULATION OPTIONS -------------
Vinf=Vinf,
rho=rho, mu=mu, sound_spd=speedofsound,
# ----- SOLVERS OPTIONS ----------------
p_per_step=p_per_step,
max_particles=max_particles,
vpm_viscous=vpm_viscous,
sigma_vlm_surf=sigma_rotor_surf,
sigma_rotor_surf=sigma_rotor_surf,
sigma_vpm_overwrite=sigma_vpm_overwrite,
vlm_rlx=vlm_rlx,
hubtiploss_correction=hubtiploss_correction,
shed_unsteady=shed_unsteady,
shed_starting=shed_starting,
extra_runtime_function=monitor_rotor,
# ----- OUTPUT OPTIONS ------------------
save_path=save_path,
run_name=run_name,
);
# ----------------- 6) VISUALIZATION -------------------------------------------
if paraview
println("Calling Paraview...")
# Files to open in Paraview
files = joinpath(save_path, run_name*"_pfield...xmf;")
for bi in 1:B
global files
files *= run_name*"_Rotor_Blade$(bi)_loft...vtk;"
files *= run_name*"_Rotor_Blade$(bi)_vlm...vtk;"
end
# Call Paraview
run(`paraview --data=$(files)`)
end
As the simulation runs, you will see the monitor shown below plotting the blade loading along with thrust and torque coefficients and propulsive efficiency.