Space Transformation Method
Complex geometries can be defined manually by applying a predefined or user-defined space transformation on a Grid object.
FLOWPanel.GeometricTools.transform!
The following predefined nonlinear orthogonal space transformations are implemented in GeometricTools:
cylindrical3D(X)cylindrical2D(X)spherical3D(X)parabolic3D(X)paraboloidal3D(X)elliptic3D(X; a=1)prolate3D(X; a=1)oblate3D(X; a=1)bipolar3D(X; a=1)toroidal3D(X; a=1)conical3D(X; b=2, c=1).
Example — Sphere, predefined transformation
import FLOWPanel as pnl
file_name = "sphere00"
save_path = "./"
# Parameters
R = 1.0 # (m) radius of sphere
P_min = [0, 0, 0] # Lower bounds of (theta, phi, dummy)
P_max = [pi, 2*pi, 0] # Upper bounds of (theta, phi, dummy)
NDIVS = [25, 50, 0] # Number of divisions (cells) of (theta, phi, dummy)
loop_dim = 2 # Coordinate to loop (1==theta)
# Generates parametric (theta, phi) grid
grid = pnl.gt.Grid(P_min, P_max, NDIVS, loop_dim)
# Transforms the grid into a spherical cartesian space
my_transform(X) = pnl.gt.spherical3D(vcat(R, X[1:2]))
pnl.gt.transform!(grid, my_transform)
# Splits the quad cells into triangular cells
dimsplit = 1
triang_grid = pnl.gt.GridTriangleSurface(grid, dimsplit)
# Save vtk and call paraview
pnl.gt.save(triang_grid, file_name; path=save_path, format="vtk")
run(`paraview --data=$(joinpath(save_path, file_name)).vtk`)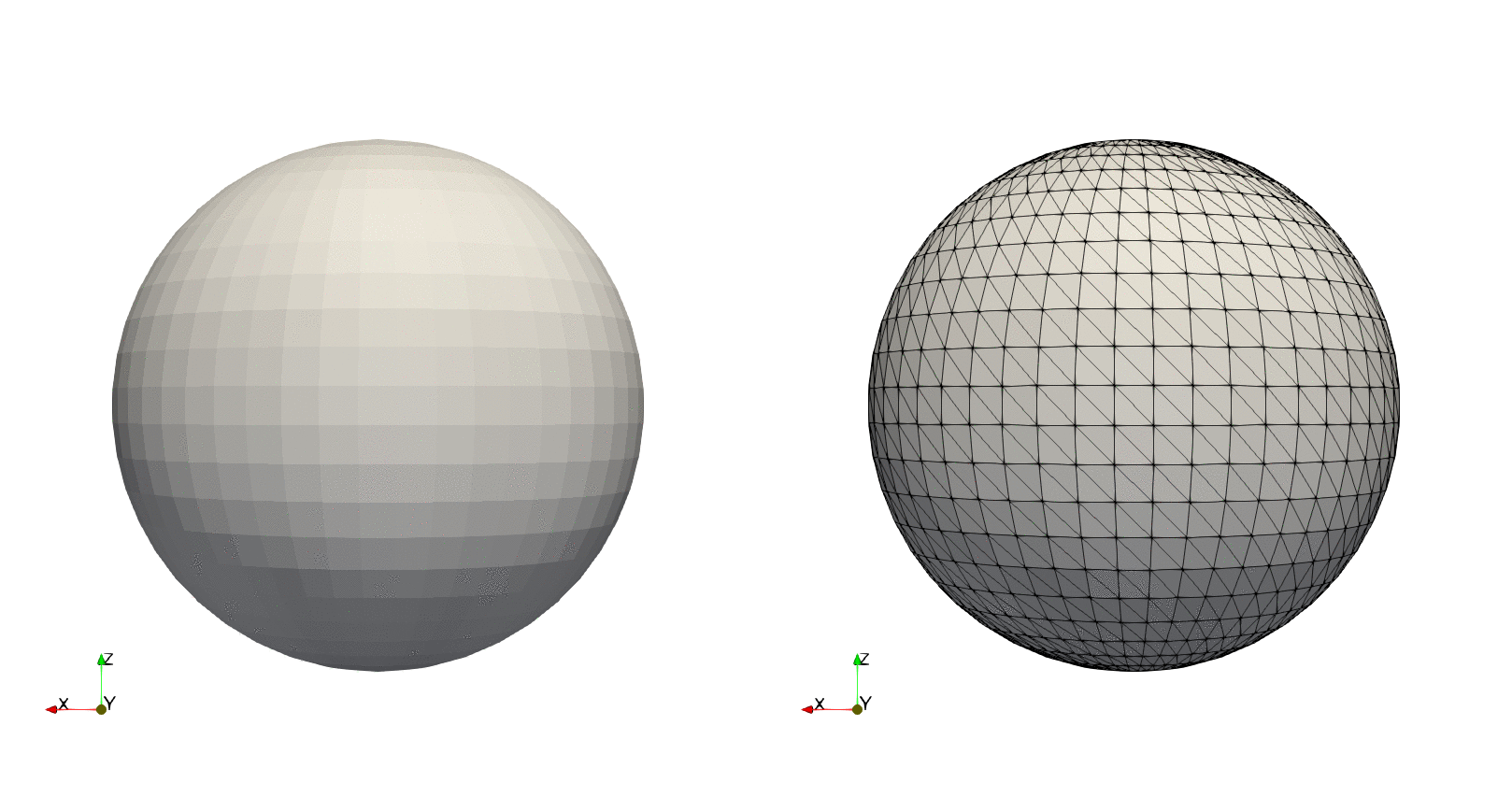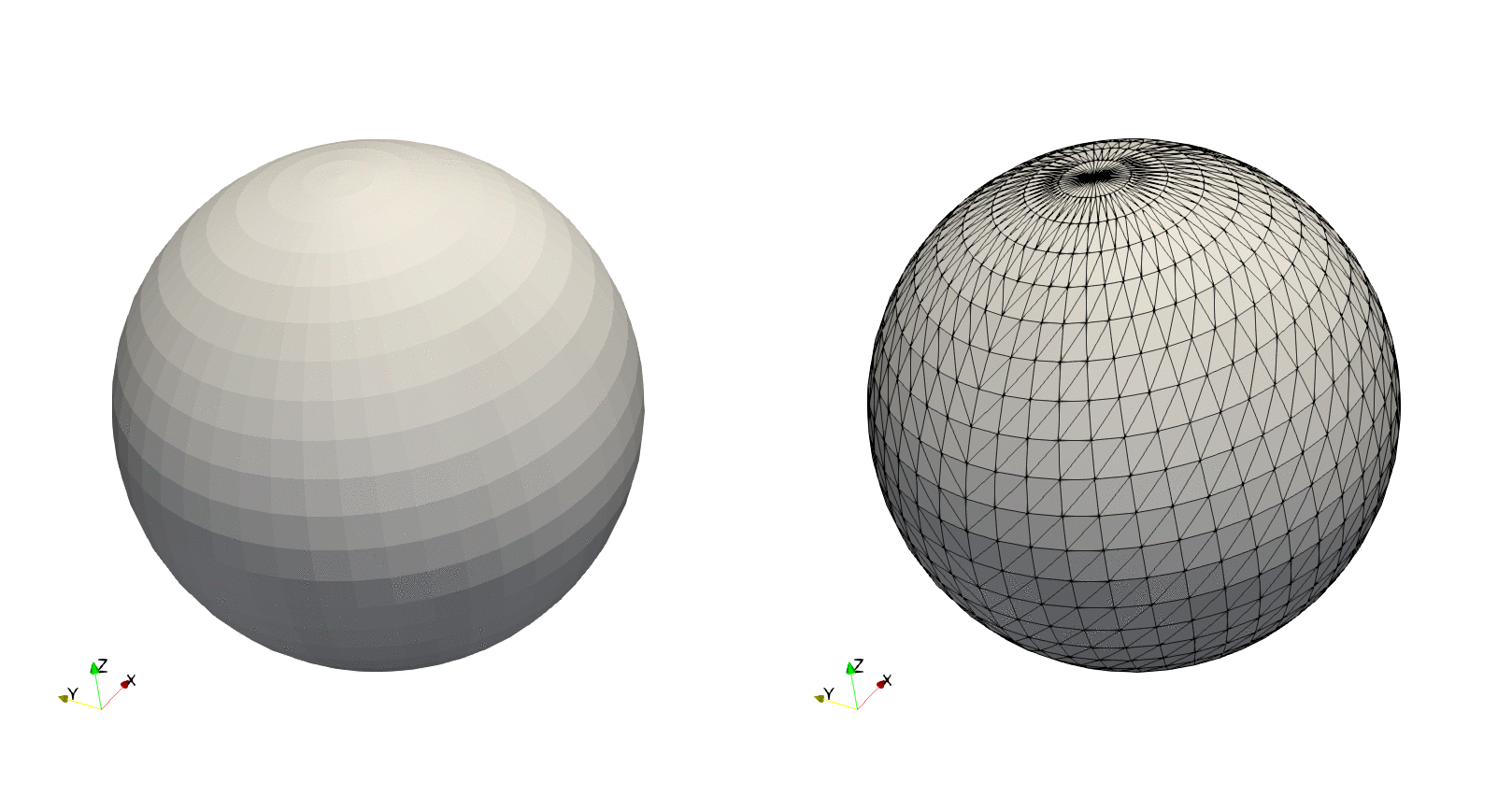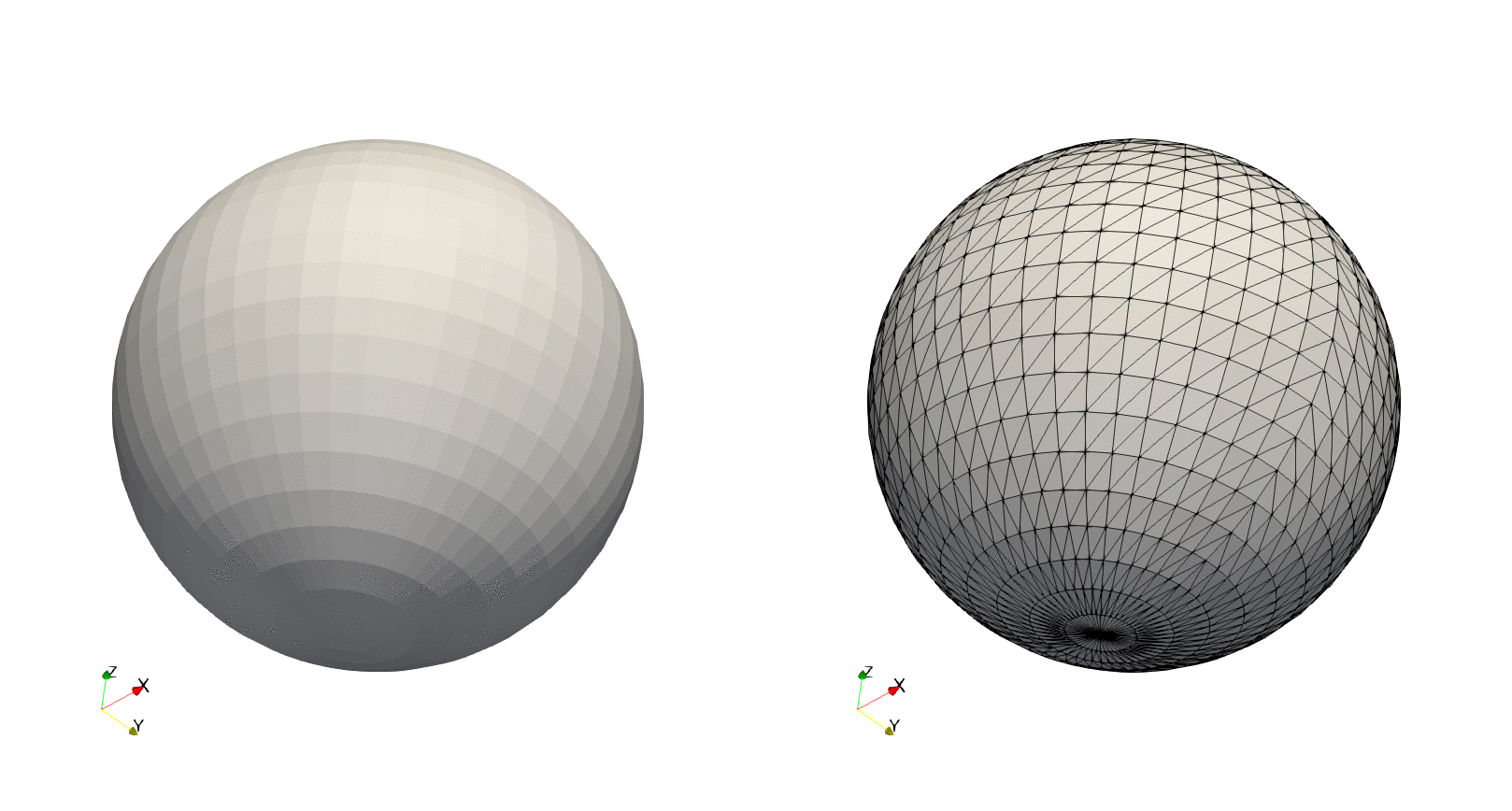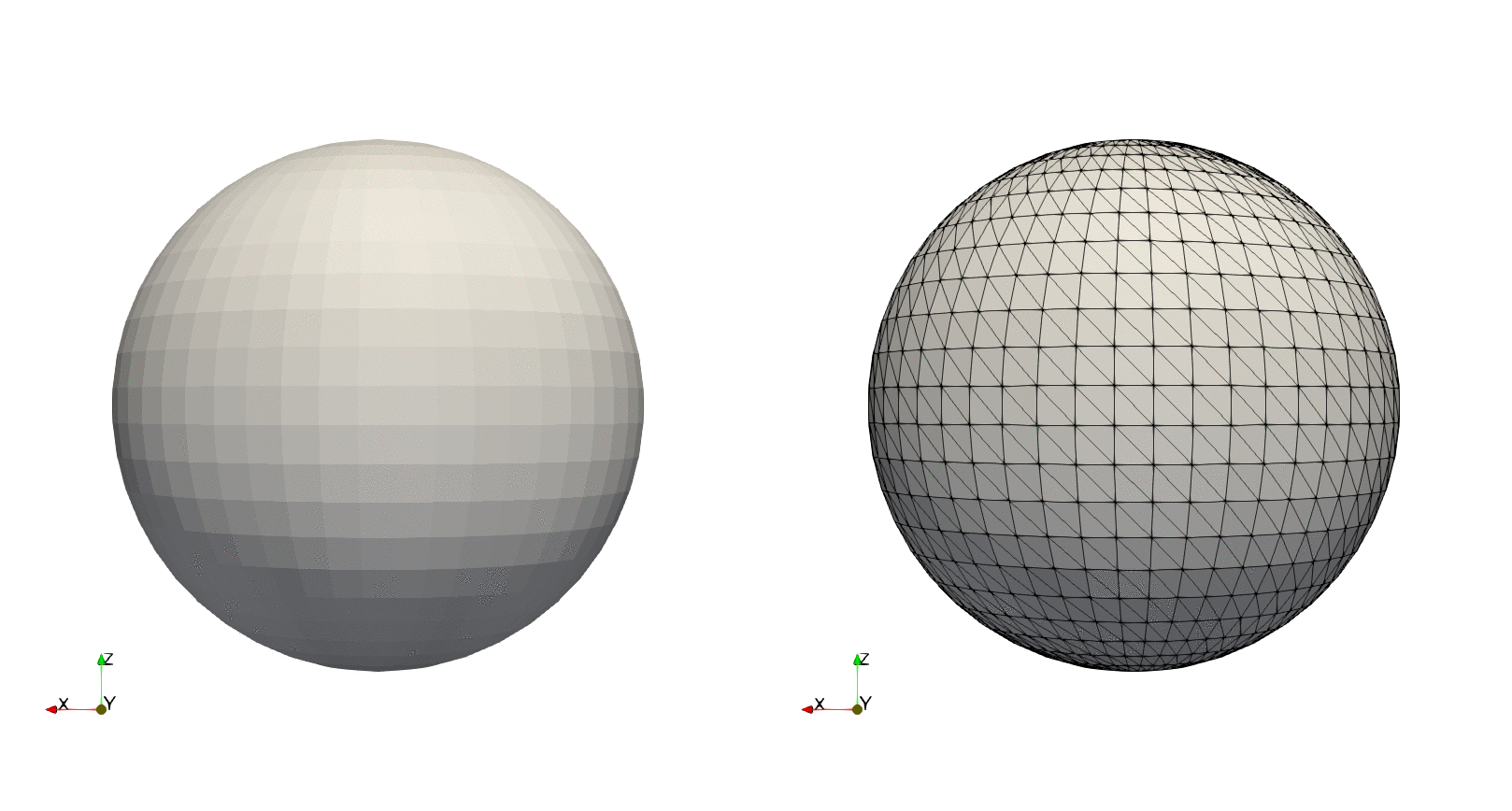
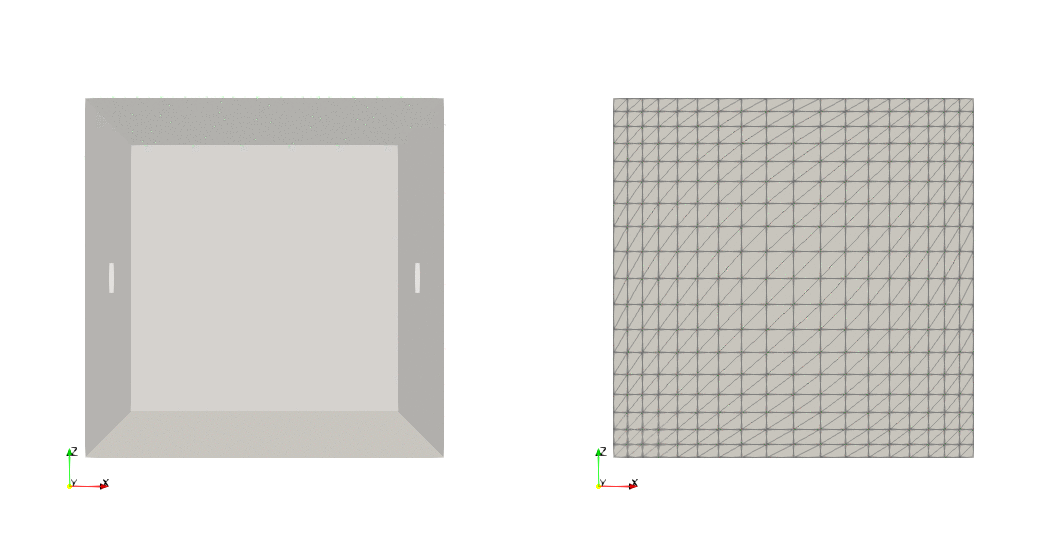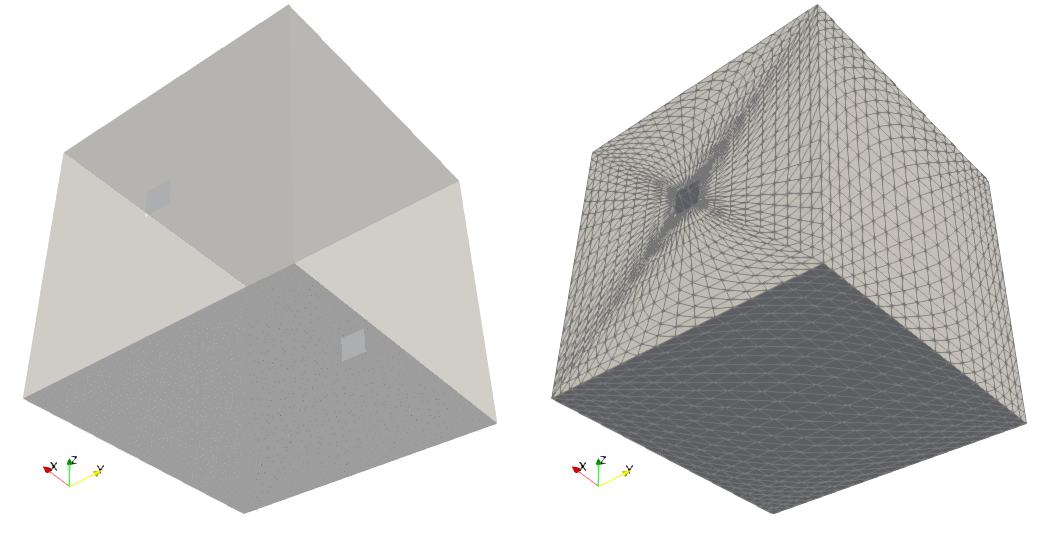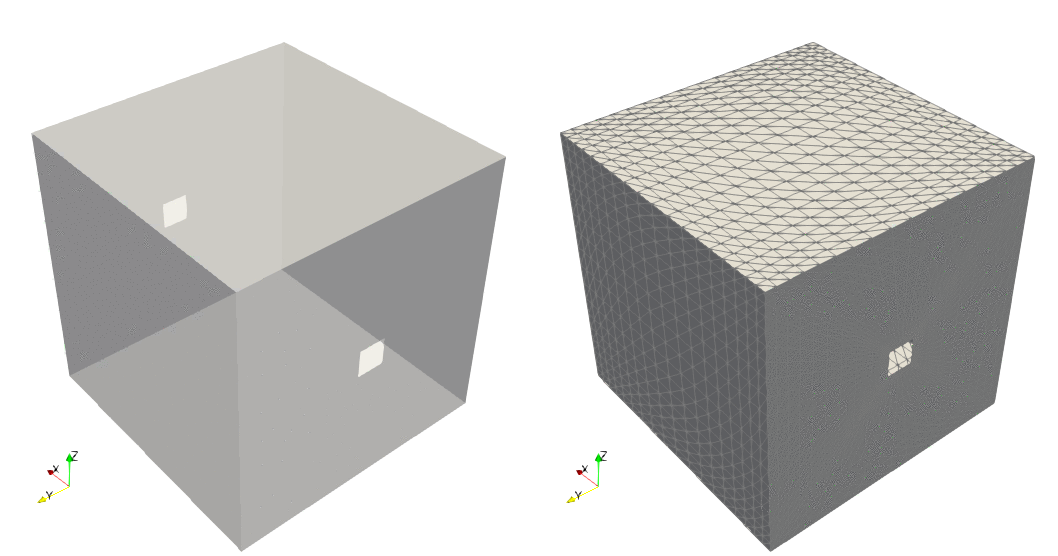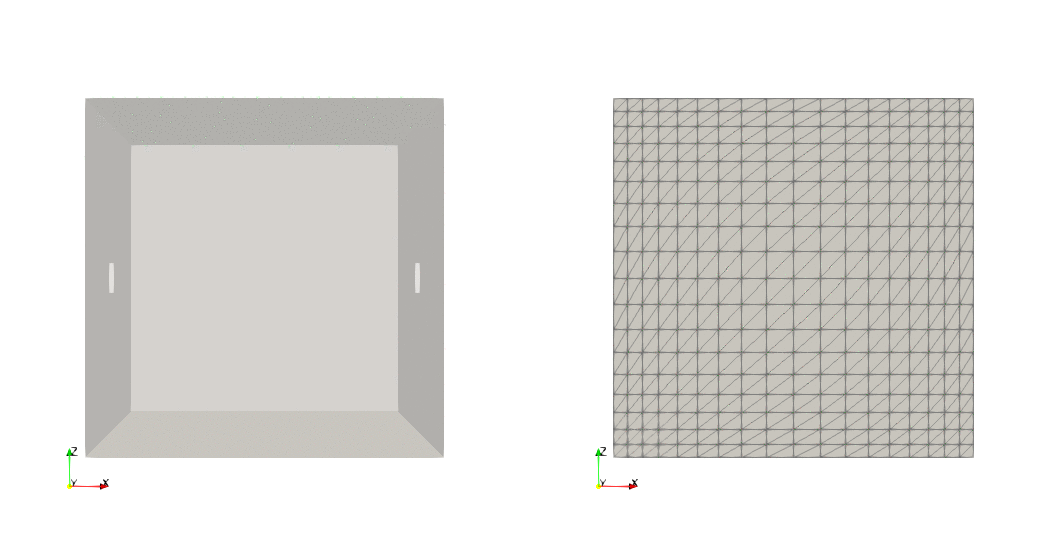
Example — Box, user-defined transformation
import FLOWPanel as pnl
file_name = "box00"
save_path = "./"
# Parameters
L = 1.0 # (m) side's length
P_min = [-0.95, 0, 0] # Lower bounds of (x, y, dummy)
P_max = [.95, 4.0, 0] # Upper bounds of (x, y, dummy)
# NDIVS = [24, 20, 0] # Number of divisions (cells) of (x, y, dummy)
N = 3
NDIVS = [
[(0.45, 3*N, 1/2, false),
(1.0, 6*N, 2.0, true),
(0.45, 3*N, 2.0, false)],
[(0.25, 6*N, 2.0, true) for i in 1:4],
[(1.0, 0, 0.0, false)]
]
loop_dim = 2 # Coordinate to loop (2==y)
# Generates parametric (theta, phi) grid
grid = pnl.gt.Grid(P_min, P_max, NDIVS, loop_dim)
# Axis on every face
Oaxis = [pnl.gt.rotation_matrix2(-a, 0, 0) for a in [90, 0, -90, -180]]
# Center of every face
O = L*[zeros(3), [0, 0, 1.0], [0, 1, 1.0], [0, 1, 0.0]]
# Axis of side sections
Oaxis_sec = [pnl.gt.rotation_matrix2(angles...)*Oaxis[i]
for (i, angles) in enumerate([(0,-90,0), (0,-90,0), (0,-90,0), (0,-90,0)])]
# Center of side sections
O_sec = [O[i]+L/2*Oaxis[i][2,:] for i in 1:4]
# Transformation function
function my_transform(X)
# Identifies the face
face = Int(floor(X[2]+1))
if face<=0 || face>4
error("Logic error! Invalid face $face")
end
# Identifies the side (-1->left, 0->center, 1->right)
side = sign(X[1])*(abs(X[1])>0.5)
if side==0
return pnl.gt.countertransform(L*[X[1], X[2]-(face-1), 0], inv(Oaxis[face]), O[face])
else
mod_X = [abs(X[1])-0.5, X[2]-(face-1)-0.5, 0]
mod_X[2] *= 1 - mod_X[1]/0.5
return pnl.gt.countertransform(L*[mod_X[1], side*mod_X[2], 0],
inv([1 0 0; 0 side 0; 0 0 side]*Oaxis_sec[face]),
O_sec[face] + L/2*[side, 0, 0])
end
end
# Converts the parametric grid into a box
pnl.gt.transform!(grid, my_transform)
# Splits the quad cells into triangular cells
dimsplit = 1
triang_grid = pnl.gt.GridTriangleSurface(grid, dimsplit)
# Save vtk and call paraview
pnl.gt.save(triang_grid, file_name; path=save_path, format="vtk")
run(`paraview --data=$(joinpath(save_path, file_name)).vtk`)