Surface Grid
A 3D surface grid can be generated by defining a 3D grid where one of its dimensions has zero divisions, and then transforming the space into the surface geometry. A dimension with zero divisions is recognized as a "quasi-dimension", which is a place holder for space transformations without actually spanning the dimensions of the grid. For instance, a 3D grid with one quasi-dimension doesn't define its cells as VTK-HEXAHEDRONs as a regular 3D grid would, but its cells are defined as VTK-QUADs. Also, quasi-dimensions are not considered as a coordinate direction, meaning that a node/cell in a 3D grid with one quasi-dimension is not indexed by three coordinates $(i,j,k)$, but with only two coordinates $(i,j)$.
The following lines exemplify the process of defining the quasi-dimensional grid, and applying the space transformation:
import GeometricTools as gt
# Create quasi-3D grid
P_min = [0, -1, 0] # Lower boundaries of arclength, span, and dummy
P_max = [1, 1, 0 ] # Upper boundaries of arclength, span, and dummy
NDIVS = [20, 10, 0] # Divisions: 20 arclength, 10 span, 0 dummy
grid = gt.Grid(P_min, P_max, NDIVS)
# Create a space transformation function
function my_space_transform(X)
new_X = ... # Write a new definition of each node here
return new_X
end
# Applie the space transformation
gt.transform!(grid, my_space_transform)Example — Paneled Wing
We will now use a space transformation on a 2D looped grid with 3D quasi-dimensions to generate the 3D surface of a wing.
import FLOWPanel as pnl
import GeometricTools as gt
# Airfoil data path
airfoil_path = joinpath(pnl.def_data_path, "airfoils");
file_name = "paneledwing00"
paraview = true
# ----------------- READ AND PARAMETERIZE AIRFOILS ----------------------------
semispan = 10 # (m) semi-span length
chords = [(0, 2.5), # (semi-span position, chord length (m))
(0.25, 2.0),
(1, 1.0)]
x_pos = [(0, 0), # (semi-span position, leading edge x-position (m))
(0.25, semispan/40 ),
(1, semispan/8 )]
z_pos = [(0, 0), # (semi-span position, leading edge z-position (m))
(0.25, semispan/100 ),
(1, semispan/50 )]
twist = [(0, 5), # (semi-span position, twist (deg))
(1, 0)]
airfoils = [(0, "naca6412.dat"), # (semi-span position, airfoil geometry)
(1, "naca6412.dat")]
airfoil_funs = []
for (pos, airfoil_file) in airfoils
# Read the original airfoil geometry from airfoiltools.com
org_x, org_y = gt.readcontour(joinpath(airfoil_path, airfoil_file); header_len=1)
# Separate upper and lower sides to make the contour injective in x
upper, lower = gt.splitcontour(org_x, org_y)
# Parameterize both sides independently
fun_upper = gt.parameterize(upper[1], upper[2], zeros(size(upper[1])); inj_var=1)
fun_lower = gt.parameterize(lower[1], lower[2], zeros(size(lower[1])); inj_var=1)
push!(airfoil_funs, [pos, (fun_upper, fun_lower)])
end
# ----------------- CREATE 3D SURFACE GRID ----------------------------------
P_min = [0, -1, 0] # Lower boundaries arclength, span, dummy
P_max = [1, 1, 0 ] # Upper boundaries arclength, span, dummy
NDIVS = [20, 10, 0] # 50 arclength cells, 10 span cells, 0 dummy
loop_dim = 1 # Loop the arclength dimension
grid = gt.Grid(P_min, P_max, NDIVS, loop_dim)
gt.plot(grid; labelnodes=!true, labelcells=!true, labelndivs=true,
fontsize=8, fig_name="org", title_str="Original Grid",
alpha=0.25)
# Auxiliary function for weighting values across span
function calc_vals(span, array)
# Finds bounding airfoil position
val_in, val_out = nothing, array[1]
for val in array[2:end]
val_in = val_out
val_out = val
if val[1]>=abs(span); break; end
end
pos_in = val_in[1]
val_in = val_in[2]
pos_out = val_out[1]
val_out = val_out[2]
weight = (abs(span)-pos_in)/(pos_out-pos_in)
return weight, val_in, val_out
end
# Creates a space transformation function
function my_space_transform(X)
span = X[2]
# Calculates chord
weight, chord_in, chord_out = calc_vals(span, chords)
chord = weight*chord_out+(1-weight)*chord_in
# Calculates airfoil geometry
weight, rfl_in, rfl_out = calc_vals(span, airfoil_funs)
fun_upper_in, fun_lower_in = rfl_in
fun_upper_out, fun_lower_out = rfl_out
# Arc-length on upper or lower side of airfoil
if X[1]<0.5
s = 1 - 2 * X[1]
fun_in = fun_upper_in
fun_out = fun_upper_out
else
s = 2 * (X[1] - 0.5)
fun_in = fun_lower_in
fun_out = fun_lower_out
end
# Point over airfoil contour
point = weight * fun_out(s) + (1 - weight) * fun_in(s)
point = chord * point
# Twist
weight, twist_in, twist_out = calc_vals(span, twist)
this_twist = weight * twist_out + (1 - weight) * twist_in
# Applies twist to the airfoil point
point = gt.rotation_matrix(-this_twist, 0, 0) * point
# Leading edge x-position
weight, x_in, x_out = calc_vals(span, x_pos)
le_x = weight * x_out + (1 - weight) * x_in
# Leading edge z-position
weight, z_in, z_out = calc_vals(span, z_pos)
le_z = weight * z_out + (1 - weight) * z_in
# Span position
y = X[2] * semispan
return [point[1] + le_x, y, point[2] + le_z]
end
# Transforms the quasi-2D grid into the wing surface
gt.transform!(grid, my_space_transform)
lims = [-semispan, semispan]
gt.plot(grid; labelnodes=!true, labelcells=!true, labelndivs=true,
fontsize=8, title_str="Transformed grid", alpha=0.25,
xlims=lims / 2 .* [0,1], ylims=lims, zlims=lims/10);
# Adds some dummy example fields
gt.add_field(grid, "node_index", "scalar", [i for i in 1:grid.nnodes], "node")
gt.add_field(grid, "cell_index", "scalar", [i for i in 1:grid.ncells], "cell")
if paraview
# Outputs a vtk file
gt.save(grid, file_name; format="vtk")
# Calls paraview
run(`paraview --data=$file_name.vtk`)
end;
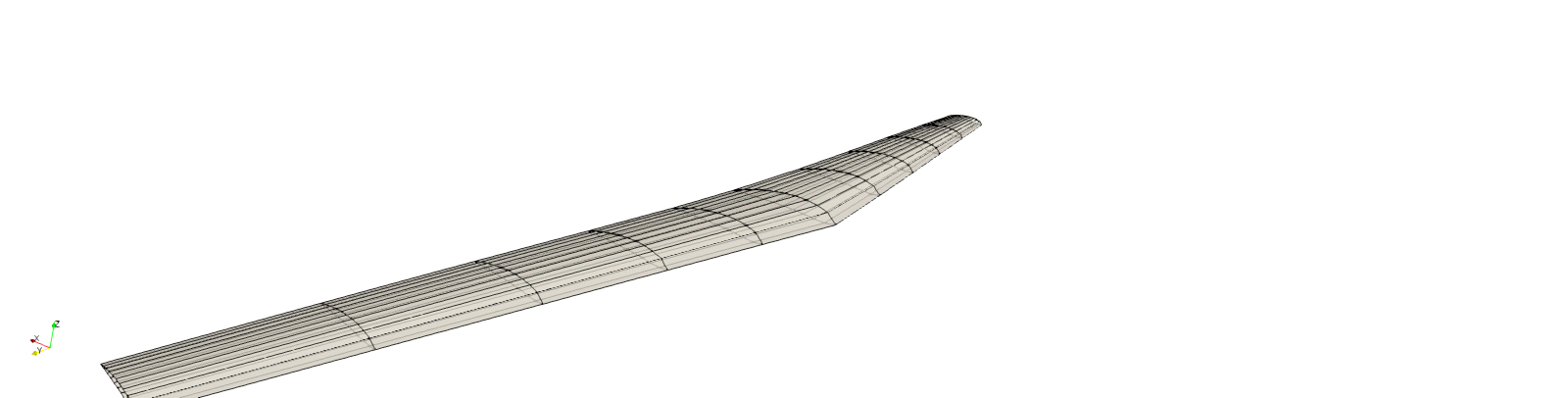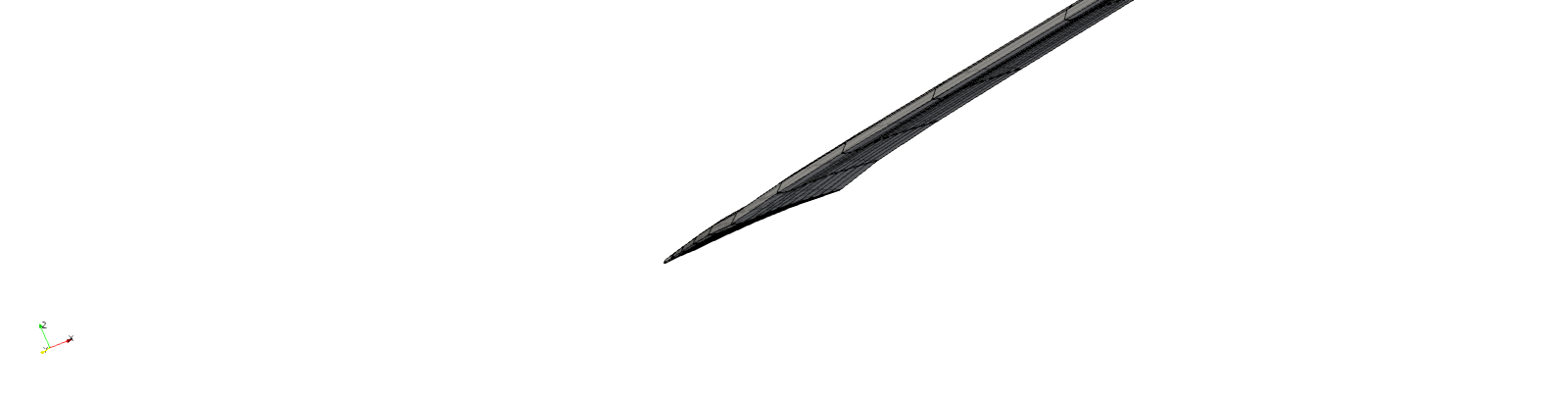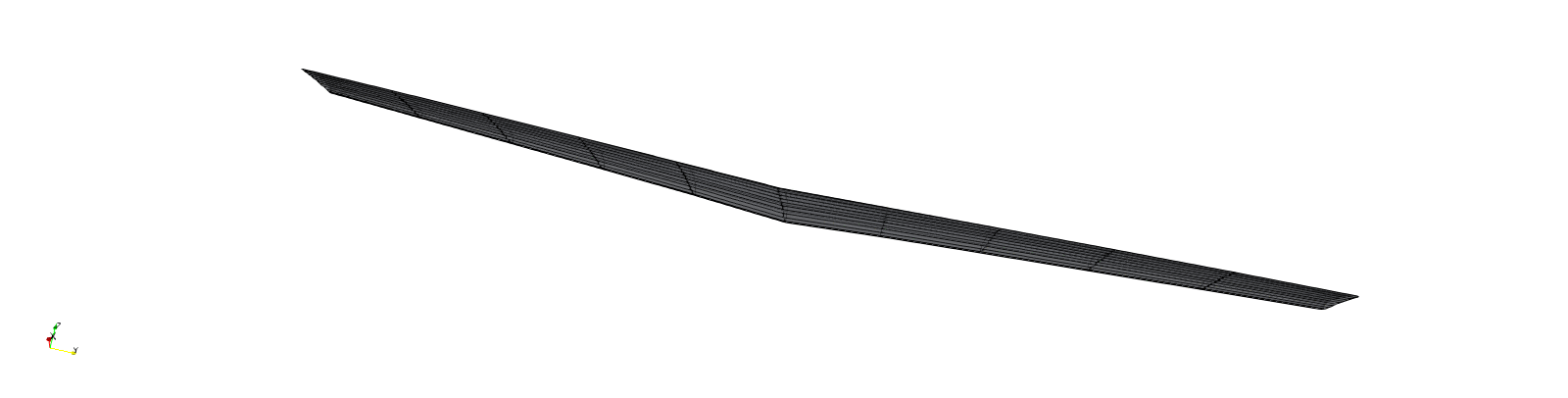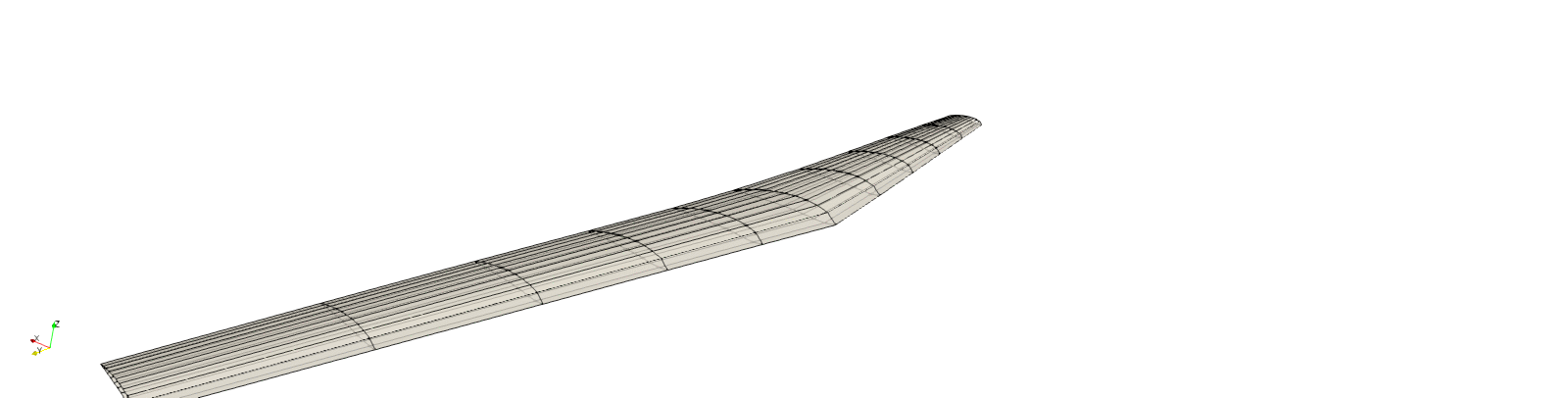
By construction, the wing we have defined has non-planar quadrilateral panel. Since some solvers require planar panels, GeometricTools has a especial type of grid that receives a 3D surface Grid object, and splits all non-planar quadrilateral panels into planar triangular panels of the VTK_TRIANGLE type.

This is implemented in the GridTriangleSurface type:
FLOWPanel.GeometricTools.GridTriangleSurface
file_name = "paneledwing01"
# Splits the quadrialateral panels into triangles
dimsplit = 1 # Dimension along which to split
triang_grid = gt.GridTriangleSurface(grid, dimsplit)
# Adds some dummy example fields
gt.add_field(triang_grid, "node_index", "scalar",
[i for i in 1:triang_grid.nnodes], "node")
gt.add_field(triang_grid, "cell_index", "scalar",
[i for i in 1:triang_grid.ncells], "cell")
gt.add_field(triang_grid, "normal", "vector",
[gt.get_normal(triang_grid, i)
for i in 1:triang_grid.ncells], "cell")
gt.add_field(triang_grid, "tangent", "vector",
[gt.get_tangent(triang_grid, i)
for i in 1:triang_grid.ncells], "cell")
if paraview
# Outputs a vtk file
gt.save(triang_grid, file_name; format="vtk")
# Calls paraview
run(`paraview --data=$file_name.vtk`)
end