Import Mesh and Solve

Here we import the mesh into FLOWPanel using Meshes.jl, identify the trailing edge, and run the watertight solver.

#=##############################################################################
# DESCRIPTION
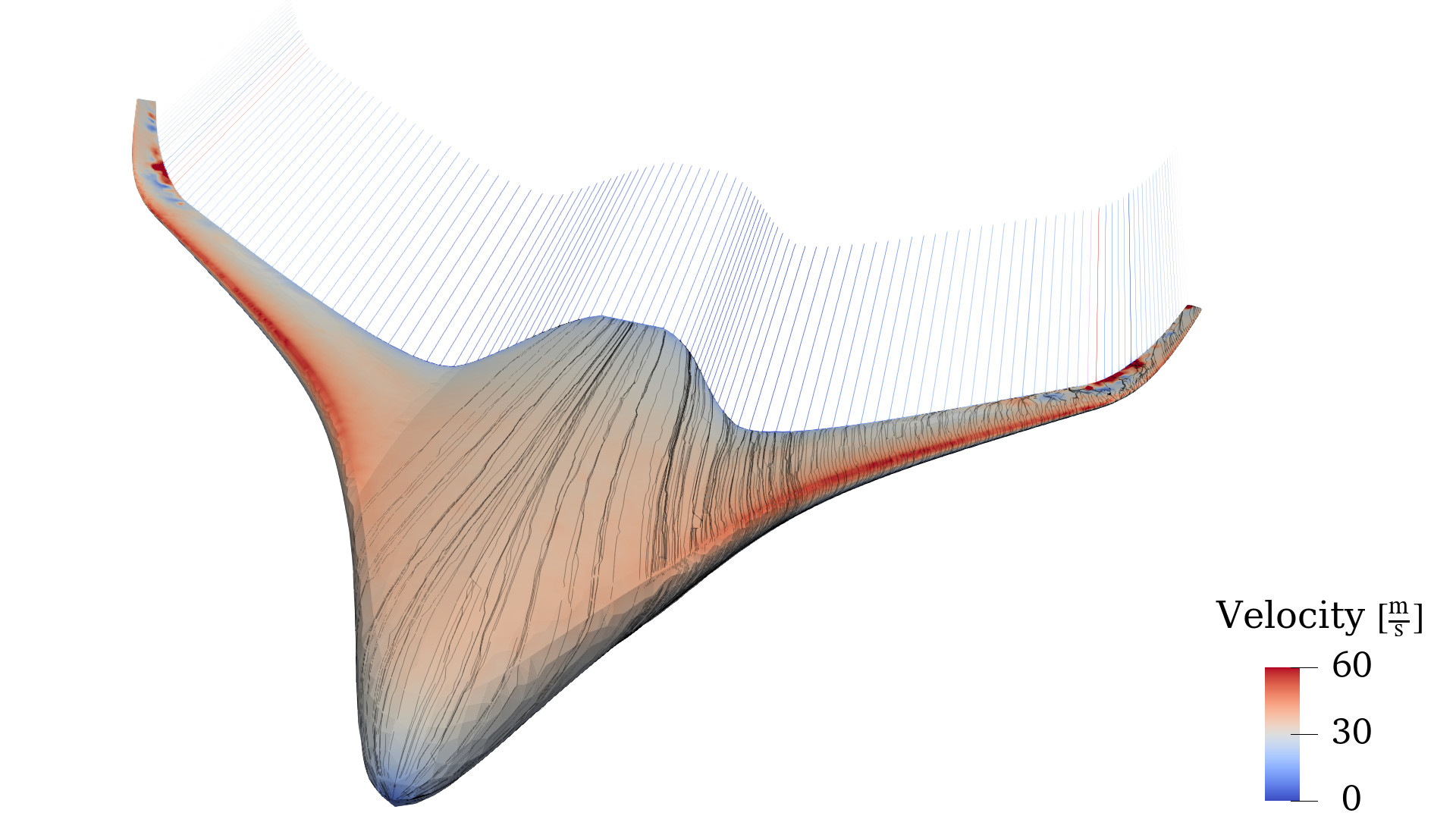
    Blended wing body resembling the Airbus ZEROe BWB twin-engine subscale
    model. The mesh used in this analysis was created using SolidWorks + Gmsh.

# AUTHORSHIP
  * Author    : Eduardo J. Alvarez
  * Email     : Edo.AlvarezR@gmail.com
  * Created   : April 2024
  * License   : MIT License
=###############################################################################

import FLOWPanel as pnl
import FLOWPanel: norm, dot, cross

import Meshes
import GeoIO
import Rotations: RotX, RotY, RotZ

# import CUDA                               # Uncomment this to use GPU (if available)


run_name        = "blendedwing"             # Name of this run

save_path       = run_name                  # Where to save outputs
paraview        = true                      # Whether to visualize with Paraview
read_path       = joinpath(pnl.examples_path, "data") # Where to read Gmsh files from

# ----------------- SIMULATION PARAMETERS --------------------------------------
AOA             = 10.0                      # (deg) freestream angle of attack
magVinf         = 30.0                      # (m/s) freestream velocity
rho             = 1.225                     # (kg/m^3) air density


# ----------------- GEOMETRY DESCRIPTION ---------------------------------------
meshfile        = joinpath(read_path, "zeroebwb.msh")    # Gmsh file to read
trailingedgefile= joinpath(read_path, "zeroebwb-TE.msh") # Gmsh file with trailing edge

symcoordinate   = 2                         # Symmetric coordinate to reflect the body (`nothing` to omit)
offset          = [0, 0, 0]                 # Offset to center the mesh
rotation        = RotZ(-90*pi/180)*RotX(90*pi/180) # Rotation to align mesh
scaling         = 2e-3                      # Factor to scale original mesh to
                                            # the approximate dimensions of the
                                            # ZEROEe BWB subscale model

spandir         = [0, 1, 0]                 # Span direction used to orient the trailing edge
flip            = false                     # Whether to flip control points against the direction of normals
                                            # NOTE: use `flip=true` if the normals
                                            #       point inside the body

Sref            = 3.23^2 / 8.0             # (m^2) reference area

# ----------------- SOLVER SETTINGS -------------------------------------------

# Solver: direct linear solver for open bodies
# bodytype = pnl.RigidWakeBody{pnl.VortexRing} # Wake model and element type

# Solver: least-squares solver for watertight bodies
bodytype        = pnl.RigidWakeBody{pnl.VortexRing, 2}

# Processing
clip_Cp         = 1 - 342.0/magVinf         # Clip pressure coefficients that are lower than this threshold


# ----------------- GENERATE BODY ----------------------------------------------
# Read Gmsh mesh
msh = GeoIO.load(meshfile)
msh = msh.geometry

# Read Gmsh line of trailing edge
TEmsh = GeoIO.load(trailingedgefile)
TEmsh = TEmsh.geometry

# Transform the original mesh: Translate, rotate, and scale
msh = msh |> Meshes.Translate(offset...) |> Meshes.Rotate(rotation) |> Meshes.Scale(scaling)

# Apply the same transformations to the trailing edge
TEmsh = TEmsh |> Meshes.Translate(offset...) |> Meshes.Rotate(rotation) |> Meshes.Scale(scaling)

# Mirror the original mesh to obtain a symmetric mesh of the airframe
if !isnothing(symcoordinate)
    msh = pnl.gt.mirror(msh, symcoordinate)
end

# Uncomment this to do 10 smoothing iterations on the mesh
# msh = msh |> Meshes.TaubinSmoothing(10)

# Wrap Meshes object into a Grid object from GeometricTools
grid = pnl.gt.GridTriangleSurface(msh)

# Convert TE Meshes object into a matrix of points used to identify the trailing edge
trailingedge = pnl.gt.vertices2nodes(TEmsh.vertices)

# Sort TE points from left to right
trailingedge = sortslices(trailingedge; dims=2, by = X -> pnl.dot(X, spandir))

# Estimate span length (used as a reference length)
spantips = extrema(X -> pnl.dot(X, spandir), eachcol(trailingedge))
span = spantips[2] - spantips[1]

# Generate TE shedding matrix
shedding = pnl.calc_shedding(grid, trailingedge; tolerance=0.001*span)

# Generate paneled body
body = bodytype(grid, shedding; CPoffset=(-1)^flip * 1e-14)

println("Number of panels:\t$(body.ncells)")


# ----------------- CALL SOLVER ------------------------------------------------
println("Solving body...")

# Freestream vector
Vinf = magVinf*[cos(AOA*pi/180), 0, sin(AOA*pi/180)]

# Freestream at every control point
Uinfs = repeat(Vinf, 1, body.ncells)

# Unitary direction of semi-infinite vortex at points `a` and `b` of each
# trailing edge panel
Das = repeat(Vinf/magVinf, 1, body.nsheddings)
Dbs = repeat(Vinf/magVinf, 1, body.nsheddings)

# Solve body (panel strengths) giving `Uinfs` as boundary conditions and
# `Das` and `Dbs` as trailing edge rigid wake direction
@time pnl.solve(body, Uinfs, Das, Dbs)

# Uncomment this to use GPU instead (if available)
# @time pnl.solve(body, Uinfs, Das, Dbs; GPUArray=CUDA.CuArray{Float32})

# ----------------- POST PROCESSING ----------------------------------------
println("Post processing...")

# Calculate surface velocity U on the body
Us = pnl.calcfield_U(body, body)

# NOTE: Since the boundary integral equation of the potential flow has a
#       discontinuity at the boundary, we need to add the gradient of the
#       doublet strength to get an accurate surface velocity

# Calculate surface velocity U_∇μ due to the gradient of the doublet strength
UDeltaGamma = pnl.calcfield_Ugradmu(body)
# UDeltaGamma = pnl.calcfield_Ugradmu(body; sharpTE=true, force_cellTE=false)

# Add both velocities together
pnl.addfields(body, "Ugradmu", "U")

# Calculate pressure coefficient (based on U + U_∇μ)
@time Cps = pnl.calcfield_Cp(body, magVinf; clip = Cp -> max(clip_Cp, Cp))

# Calculate the force of each panel (based on Cp)
@time Fs = pnl.calcfield_F(body, magVinf, rho)

# Calculate total force of the vehicle decomposed as lift, drag, and sideslip
Dhat = Vinf/norm(Vinf)                      # Drag direction
Shat = [0, 1, 0]                            # Span direction
Lhat = cross(Dhat, Shat)                    # Lift direction

LDS = pnl.calcfield_LDS(body, Lhat, Dhat)

L = LDS[:, 1]
D = LDS[:, 2]

# Force coefficients
nondim = 0.5*rho*magVinf^2*Sref             # Normalization factor
CL = sign(dot(L, Lhat)) * norm(L) / nondim
CD = sign(dot(D, Dhat)) * norm(D) / nondim

@show L
@show D
@show CL
@show CD

# ----------------- VISUALIZATION ------------------------------------------

# Save body as VTK
vtks = save_path*"/"                        # String with VTK output files
vtks *= pnl.save(body, run_name; path=save_path)

# Call Paraview
if paraview
    run(`paraview --data=$(vtks)`)
end

import FLOWPanel as pnl

include(joinpath(pnl.examples_path, "blendedwingbody.jl"))